What was the original proof that Pythagoras himself used to prove his theorem?
1 Answer
We don't know. The fact is that the existence of Pythagoras is kind of a mystery itself.
There's a legend about how Pythagoras discovered "his" theorem.
Explanation:
The legend tells that Pythagoras was looking at the square tiles of Samos' palace, waiting to be received by Polycrates, when he noticed that if one divides diagonally one of those squares, it turns out that the two halves are right triangles (whose area is half the area of the tile).
The area of a square whose side is the hypotenuse of one of those right triangles, is double the area of a square tile. Here's an image that shows this (the dashed square is made of 4 half tiles, i.e. 2 tiles in total)
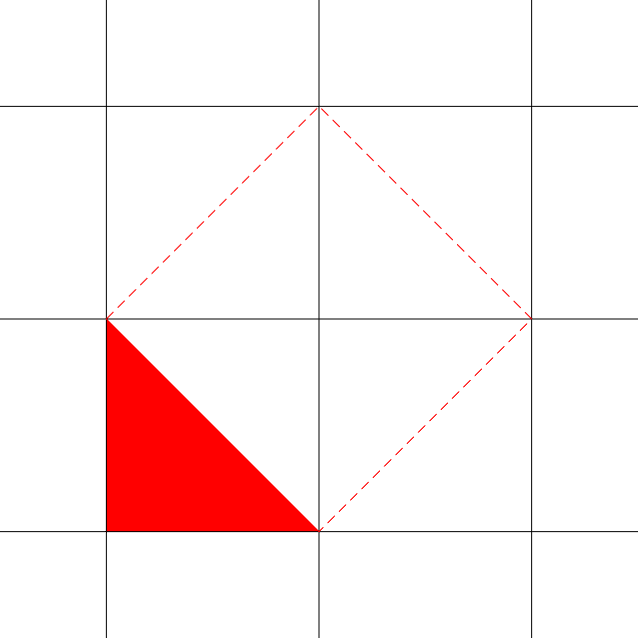
Now, since the two legs of the right triangle are sides of a tile, the squares built on them are two tiles. Hence, the sum of their area equals the area of the square built on the hypotenuse (the dashed one). So Pythagoras' theorem holds for isosceles right triangles.
The legend tells that, after proving this result, Pythagoras generalized his theorem, to make it hold for right triangles whose sides are not equal.
He concentrated his attention on the 4 tiles on which the square built on the hypotenuse was constructed, and he noticed that the drawing could be modified in the following way (on the left the former drawing, on the right the modified version):
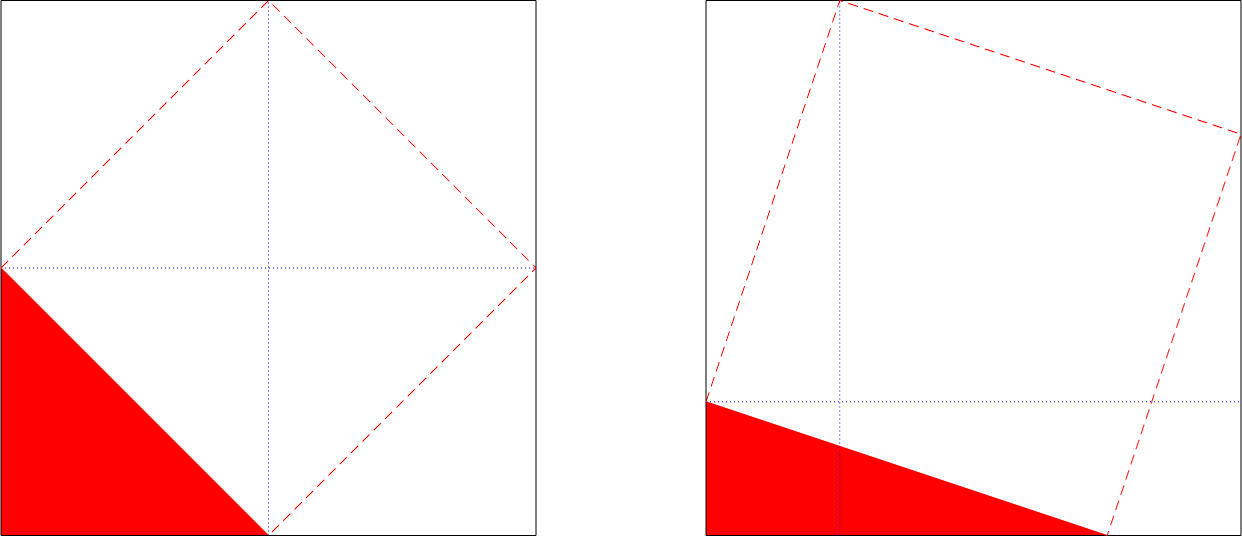
In the right image, the two squares built on the legs of the red-filled right triangle are equivalent to the two squares delimited by the blue dots. Each of the two remaining rectangles, delimited by the blue dots, is made by two copies of the red-filled triangle. Together, the two squares and the two rectangles build 4 tiles (the surrounding square). So the surrounding square is made by the two squares built on the legs and 4 copies of the red-filled right triangle.
Another way to divide the surrounding square is to consider the square built on the hypotenuse (the dashed one). On each side of this square there's a copy of the red-filled right triangle. So the surrounding square can be also built using the dashed square and 4 copies of the red-filled right triangle.
In both ways of constructing the surrounding square we used 4 copies of the red-filled right triangle. This means that if we "subtract" those copies from both the constructions, we are left with two equivalent (i.e. same total area) sets of figures. One set is made by the two squares built on the legs, the other one is made by the square built on the hypotenuse. This proves the theorem!
Historical note
The reality is that we are not sure that Pythagoras even existed. The ancient descriptions idealize him so much that he's always depicted as a son of gods.
The sure fact is that Pythagoras was not the first that discovered "his" theorem. In China, for example, a proof of the theorem was known around 1000 years before Pythagoras birth and is contained in one of the oldest Chinese mathematical texts: Zhou Bi Suan Jing.
Even in the Shulba Sutras, Indian ancient texts written before Pythagoras' birth, contain a proof of the theorem.
Babylonians knew the theorem too.
There are a lot of ways to prove Pythagorean theorem. You can find a bunch of them (and a lot of further information) on this (wonderful) website: Cut The Knot - Pythagorean Theorem.

