the area of the polar curve given by:
color(red)[A=1/2int_(theta_1)^(theta_2)r^2*d(theta)
The interval of the integral theta in [pi/8,pi/4]
now lets setup the integral in our interval:
A=1/2int_(pi/8)^(pi/4)(8sin(3theta-(2pi)/4) +4theta)^2*d(theta)
A=1/2int_(pi/8)^(pi/4)(4theta-8cos(3theta))^2*d(theta)
A=1/2int_(pi/8)^(pi/4)(4theta-8cos(3theta))^2*d(theta)
A=int_(pi/8)^(pi/4)[8(theta)^2-32thetacos(3theta)+32cos^2(3theta)]*d(theta)
=[(24sin(6theta)-96xsin(3theta)-32cos(3theta)+24theta^3+144theta)/9]_(pi/8)^(pi/4)
[(3*2^(21/2)pisin((3pi)/8)+2^(27/2)*cos((3pi)/8)+21*2^(5/2)pi^3+(9*2^(19/2)-6144)pi-3*2^(23/2)+2048)/(9*2^(17/2))]=4.68224
Approximation:
A=4.68224
see below the sketch of the polar curve:
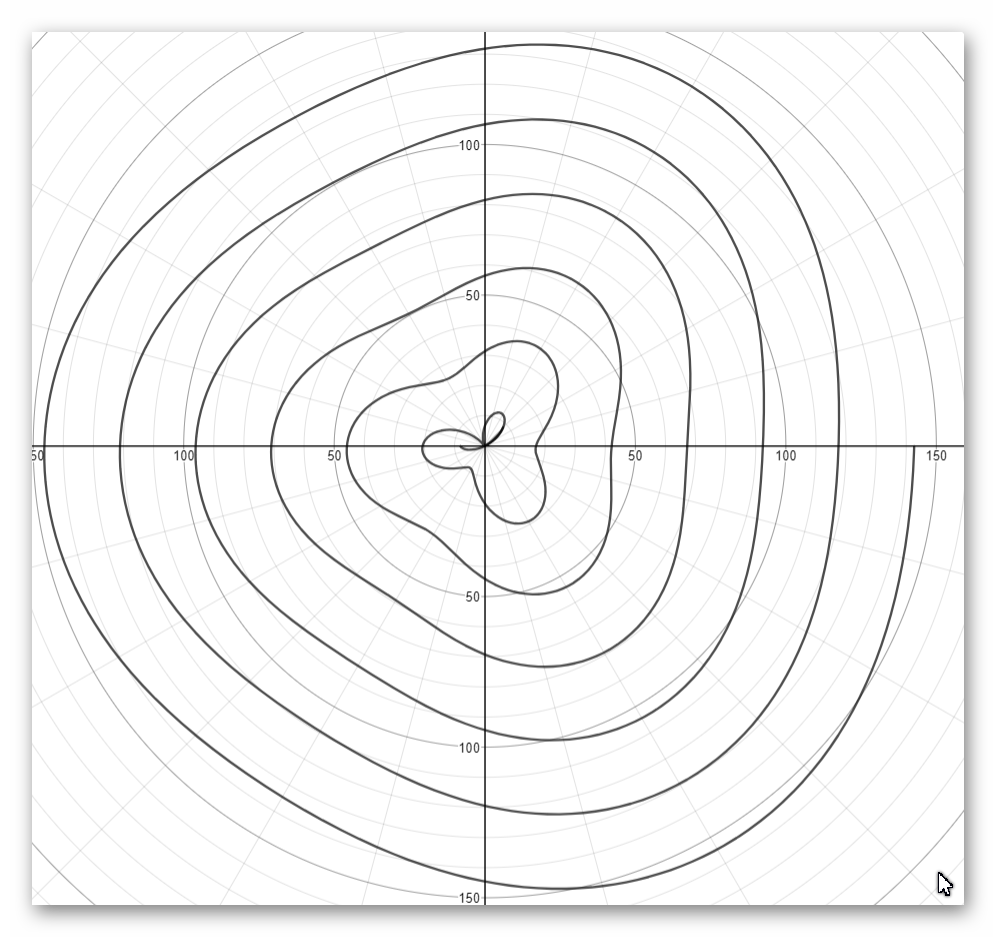 james
james
see below the region bounded by the curve from pi/8 topi/4
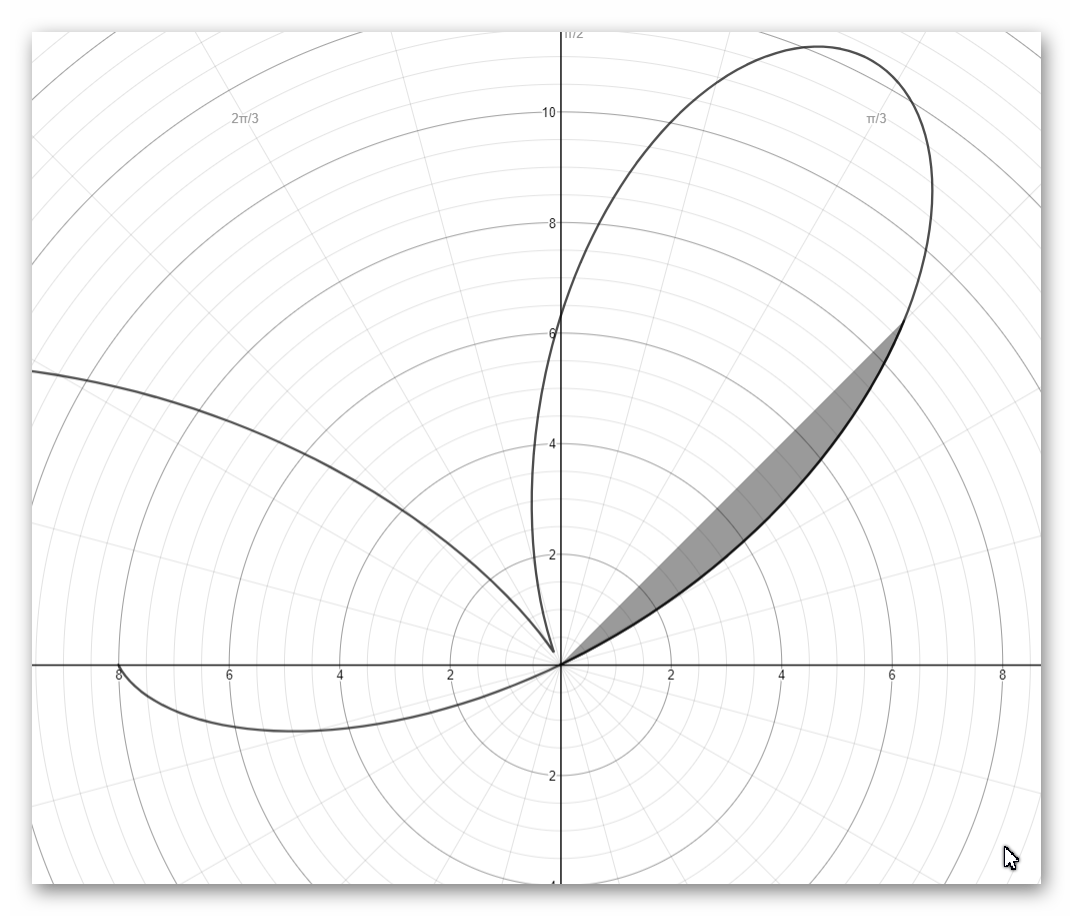 james
james
"I hope that helpful"
 james
james  james
james 
