Question

What is the area of a regular octagon with a side of 8 inches?

Answer 1

Area of a regular octagon with a side of `8` inches is `309.02` square inches.

Explanation:

An octagon has all its angles `135^@`. Hence if we extend its four alternate sides, it will form a square as shown.

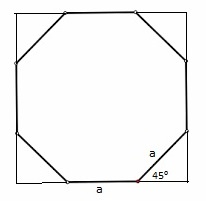
Observe that this forms four right angled isosceles triangles, with hypotenuse of size `a` and other two sides of triangle would be `a/sqrt2` (as then their squares will be `a^2/2` and `a^2/2+a^2/2=a^2`, the square on the hypotenuse).

Hence area of each triangle is `1/2xx(a/sqrt2)^2=1/2xxa^2/2=a^2/4`

and area of all the four triangle is `a^2`.

Now each side of outer square is `a+(a/sqrt2xx2)`

= `a+asqrt2`

and its area is `(a+asqrt2)^2=a^2(1+sqrt2)^2`

= `a^2(1+2+2sqrt2)=a^2(3+2sqrt2)`

and hence area of octagon is area of square minus area of four triangles i.e.

`a^2(3+2sqrt2)-a^2=2a^2(1+sqrt2)`

Hence, area of a regular octagon with a side of `8` inches is

`2xx8^2(2+2sqrt2)=2xx64(1=sqrt2)=128xx2.4142=309.02` square inches.