What is the area of a triangle with vertices (x_1, y_1), (x_2, y_2), (x_3, y_3) ?
2 Answers
Explanation:
Given three vertices:
Start by assuming:
x_1 < x_3 < x_2
y_1 < y_2 < y_3
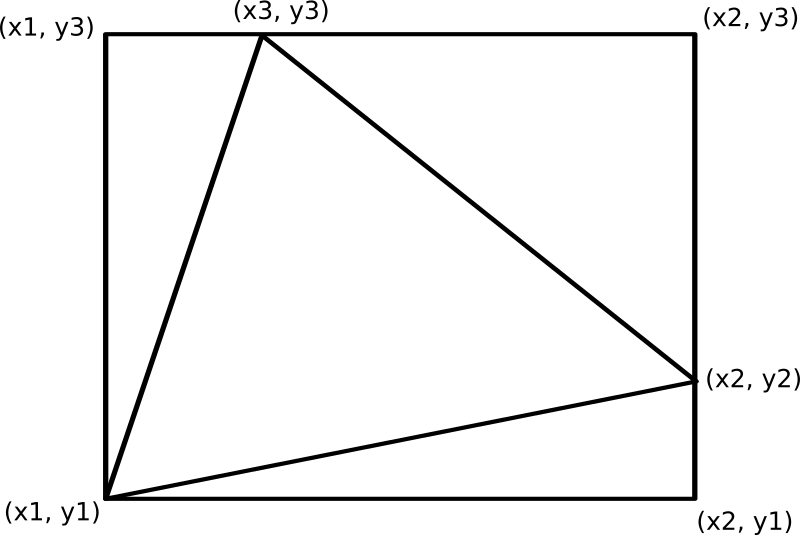
The triangle can be drawn in a rectangle with vertices:
(x_1, y_1) ,(x_2, y_1) ,(x_2, y_3) ,(x_1, y_3)
dividing it into
-
(x_1, y_1) ,(x_2, y_1) ,(x_2, y_2) with area:1/2 (x_2-x_1)(y_2-y_1) -
(x_2, y_2) ,(x_2, y_3) ,(x_3, y_3) with area:1/2 (x_2-x_3)(y_3-y_2) -
(x_3, y_3) ,(x_1, y_3) ,(x_1, y_1) with area:1/2 (x_3-x_1)(y_3-y_1)
So the area of the given triangle is:
(x_2-x_1)(y_3-y_1) - 1/2 (x_2-x_1)(y_2-y_1) - 1/2 (x_2-x_3)(y_3-y_2) - 1/2 (x_3-x_1)(y_3-y_1)
=1/2 (x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2)
Note the symmetry of the final expression. It is symmetric in
If we are only interested in the unsigned area of the triangle then we can ignore our initial assumptions and write the universal formula:
"Area" = 1/2 abs(x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2)
Just a small comment to the answer from George C.
Explanation:
The answer from George C. is 100% right, even for triangles with such vertices, that they do not fit on a rectangle. An example would be a triangle with the vertices
GeoGebra
Even if the rectangle does not fit, we can still apply the formular and get the solution.


