What is the area of the largest isosceles triangle that can be inscribed in a circle of radius 4?
1 Answer
Explanation:
One could start by saying that the isosceles triangle with largest area inscribed in a triangle is also an equilateral triangle.
However if you need a formal demonstration of this statement read the first part of this explanation.
Suppose an isosceles
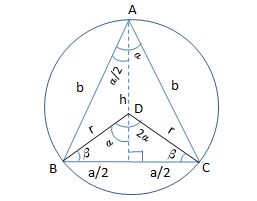 I created this figure using MS Excel
I created this figure using MS Excel
We can obtain the side
a/sin(2alpha)=r/sin beta
Since2alpha+beta+beta=180^@ =>beta=90^@-alpha
=>a=rsin (2alpha)/sin(90^@-alpha)=2r(sin alpha *cancel(cos alpha))/cancel(cos alpha)
=>a=2rsin alpha=4rsin (alpha/2)cos (alpha/2)
We can obtain the height
tan(alpha/2)=(a/2)/h =>h=a/(2tan(alpha/2))
Replacinga for its value in function ofr andalpha :
h=(4rcancel(sin(alpha/2))cos(alpha/2))/2*cos(alpha/2)/cancel(sin(alpha/2))
=>h=2rcos^2(alpha/2)
Then we can obtain the area of the triangle in function of
S_(triangle_(ABC)) =("base"*"height")/2
S_(triangle_(ABC))=((4rsin(alpha/2)cos(alpha/2))(cancel(2)rcos^2(alpha/2)))/cancel(2)
S_(triangle_(ABC))=4r^2 sin(alpha/2)cos^3(alpha/2)
Since in this problem
So
d/(dalpha)(S_(triangle_(ABC)))=4r^2 cos(alpha/2)*(1/2)cos^3(alpha/2)+4r^2 sin(alpha/2)*3cos^2(alpha/2)(-sin(alpha/2))(1/2)
=2r^2cos^4(alpha/2)-6r^2sin^2(alpha/2)cos^2(alpha/2)
=2r^2cos^2(alpha/2)(cos^2(alpha/2)-3sin^2(alpha/2))
Equating the derivative to zero we get:
cos^2(alpha/2)=0 =>cos (alpha/2)=0 =>alpha/2=90^@ =>alpha=180^@ (this is the point of minimum area)
And
cos^2(alpha/2)-3sin^2(alpha/2)=0 =>3sin^2(alpha/2)=cos^2(alpha/2) =>tan(alpha/2)=1/sqrt(3) =>alpha/2=30^@ =>alpha=60^@ (this is the point of maximum area)
-> But ifalpha=60^@ this means thatAhatBC=AhatCB=60^@ and the isosceles triangle of maximum area is also an equilateral triangle.
Area of the triangle of maximum area
S_(triangle_(ABC))=4*4^2sin 30^@*cos^3 30^@=4*16*(1/2)(sqrt(3)/2)^3=32*(3sqrt(3))/8=12sqrt(3)~=20.784

