To transform an expression in polar form to Cartesian (or rectangular) form, we need the formulas that relate #r# and #theta# to #x# and #y#.
Step 1. Recall the relationships between polar and Cartesian.
#x^2+y^2=r^2#
#x=rcos(theta)# or #cos(theta)=x/r# or #theta=cos^-1(x/r)#
#y=rsin(theta)# or #sin(theta)=y/r# or #theta=sin^-1(y/r)#
#tan(theta)=y/x#
These relationships can be determined from drawing a point in one of two ways, as radius and angle or as #x#-coordinate and #y#-coordinate as seen below.
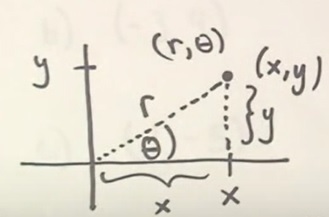
Step 2. Convert each term from polar to Cartesian.
We are given #r-5theta=sin^3(theta)+sec(theta)#. Let's take each part and put it terms of #x# and #y#.
#r=sqrt(x^2+y^2)#
#5theta=5sin^-1(y/r)#
Plugging #r=sqrt(x^2+y^2)# into the previous gives
#5theta=5sin^-1(y/sqrt(x^2+y^2))#
#sin^3(theta)=(y/r)^3=(y/sqrt(x^2+y^2))^3#
#sec(theta)=1/cos(theta)=r/x=sqrt(x^2+y^2)/x#
Step 3. Plug these back into the original.
#r-5theta=sin^3(theta)+sec(theta)# becomes
#sqrt(x^2+y^2)-5sin^-1(y/sqrt(x^2+y^2))=(y/sqrt(x^2+y^2))^3+sqrt(x^2+y^2)/x#
You could spend a lot of time trying to simplify and trying to find a function #y# in terms of the independent variable #x#, but this is not what your question asked. So this is a great place to stop!

