What is the Cartesian form of #r-theta = -2sin^2theta-cot^3theta #?
1 Answer
Mar 20, 2016
Set:
Answer is:
Explanation:
According to the following picture:
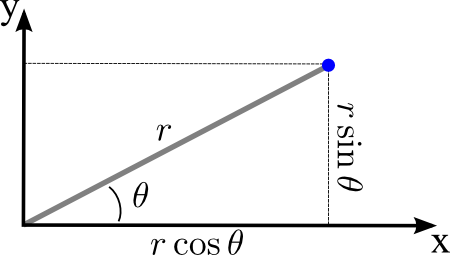
Set:
So we have:
The equation becomes:
