I can't completely agree with Gió's answer, because it's incomplete and also (formally) wrong.
The formal error is in the usage of De Moivre's formula with non-integer exponents. De Moivre's formula can be applied to integer exponents only. More details on this on the Wikipedia's page
There you'll find a partial extension of the formula, to deal with #n#-th roots (it involves an extra-parameter #k#): if #z=r(cos theta+i sin theta)#, then
#z^{1/n}=r^{1/n}(cos ((theta+2 k pi)/n) + i sin ((theta+2 k pi)/n))# where #k=0, ..., n-1#.
One (and in some sense the) very fundamental property of complex numbers is that #n#-th roots have... #n# roots (solutions)! The parameter #k# (that varies between #0# and #n-1#, so #n# values) lets us summarize them in a single formula.
So cube roots have three solutions and finding just one of them is not enough: it's just "#1/3# of the solution".
I'll write my solution-proposal below. Comments are welcome!
As Gió correctly suggested, the first step is expressing #z=sqrt{3}-i# in its trigonometric form #r(cos theta+i sin theta)#. When dealing with roots, the trigonometric form is (almost) always an useful tool (together with the exponential one). You get:
#r=sqrt{x^2+y^2}=sqrt{(sqrt{3})^2+(-1)^2}=sqrt{3+1}=sqrt{4}=2#
#theta=arctan(y/x)=arctan(- 1/sqrt{3})=-pi/6#
So #z=r(cos theta + i sin theta)=2(cos (-pi/6)+i sin(-pi/6))#
Now you want to compute the roots. By the formula reported above, we get:
#z^{1/3}=r^{1/3}(cos ((theta+2 k pi)/3)+i sin ((theta+2 k pi)/3))=2^{1/3}(cos ((-pi/6+2 k pi)/3)+i sin ((-pi/6+2 k pi)/3))#
where #k=0, 1, 2#. So there are three different values of #k# (#0#, #1# and #2#) that give birth to three different complex roots of #z#:
#z_0=2^{1/3}(cos ((-pi/6+0)/3)+i sin ((-pi/6+0)/3))=2^{1/3}(cos (-pi/18)+i sin (-pi/18))#
#z_1=2^{1/3}(cos ((-pi/6+2 pi)/3)+i sin ((-pi/6+2 pi)/3))=2^{1/3}(cos (-11/18 pi)+i sin (-11/18 pi))#
#z_2=2^{1/3}(cos ((-pi/6+4 pi)/3)+i sin ((-pi/6+4 pi)/3))=2^{1/3}(cos (-23/18 pi)+i sin (-23/18 pi))#
#z_0#, #z_1# and #z_2# are the three solutions.
The geometric interpretation of the formula for the #n# roots is very useful to draw the solutions in the complex plane. Also the plot points out very nicely the properties of the formula.
First of all, we can notice that all the solutions have the same distance #r^{1/n}# (in our example #2^{1/3}#) from the origin. So they all lie on a circumference of radius #r^{1/n}#. Now we have to point out where to place them on this circumference. We can rewrite the arguments of sine and cosine in the following way:
#z^{1/n}=r^{1/n}(cos (theta/n+(2pi)/n k)+i sin (theta/n+(2pi)/n k))#
The "first" root corresponds to #k=0#:
#z_0=r^{1/n}(cos (theta/n)+i sin (theta/n))#
All the other roots can be obtained from this by adding the angle #(2pi)/n# recursively to the angle #theta/n# relative to the first root #z_0#. So we are moving #z_0# on the circumference by a rotation of #(2pi)/n# radians (#(360°)/n#). So the points are located on the vertices of a regular #n#-gon. Given one of them, we can find the others.
In our case:
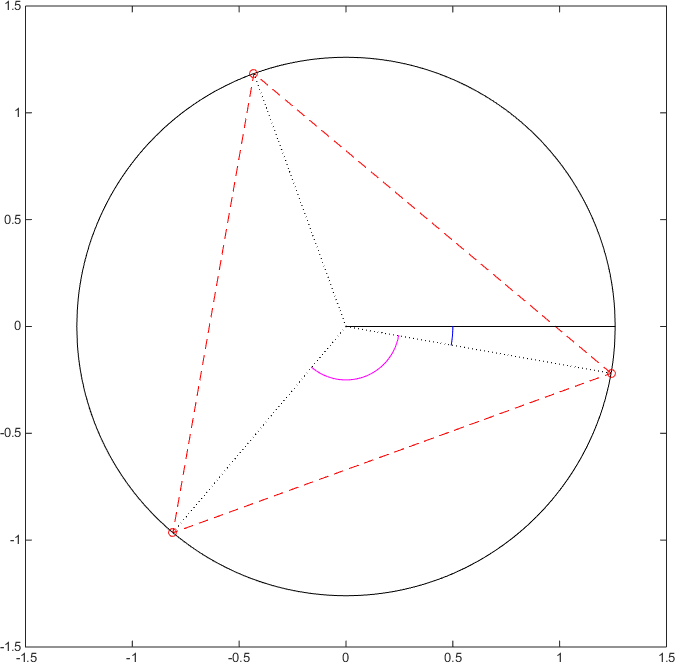
where the blue angle is #theta/n=-pi/18# and the magenta one is #(2pi)/n=2/3 pi#.