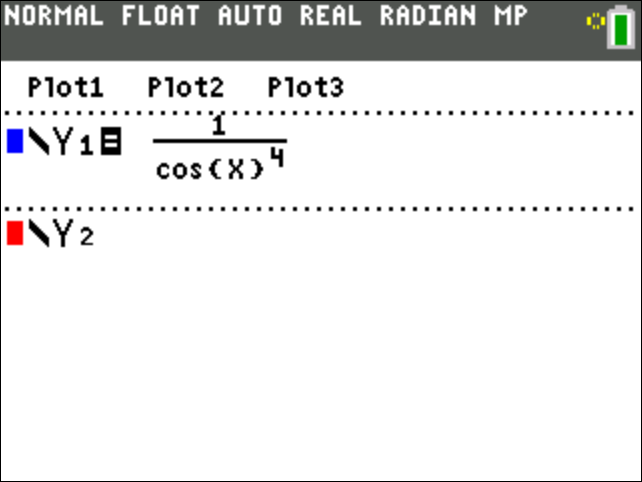
What is the definite integral of #sec^4 x# from 0 to #pi/4#?

Question

17320 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2014-09-30T05:09:32

#int_0^(pi/4)sec^4(x)dx=int_0^(pi/4)sec^2(x)sec^2(x)dx#

Trig Identity

#sec^2(x)=tan^2(x)+1#

Use this identity to substitute for one of the #sec^2(x)#.

#int_0^(pi/4)[tan^2(x)+1]sec^2(x)dx#

Now begin with u-substitution

Let #u=tan(x)#

#du=sec^2(x) dx#

#int[u^2+1] du#

#[u^3/3+u]# Convert back to terms of x #-> [tan(x)^3/3+tan(x)]_0^(pi/4)#

#=[tan(pi/4)^3/3+tan(pi/4)-(tan(0)/3+tan(0))]#

#=[(1)^3/3+1-(0+0)]#

#=[1/3+1]#

#=[1/3+3/3]#

#=[4/3]#

#=1.3333#

Remember that, #sec(x)=1/cos(x)#

So we can also say, #sec^4(x)=1/(cos^4(x))#

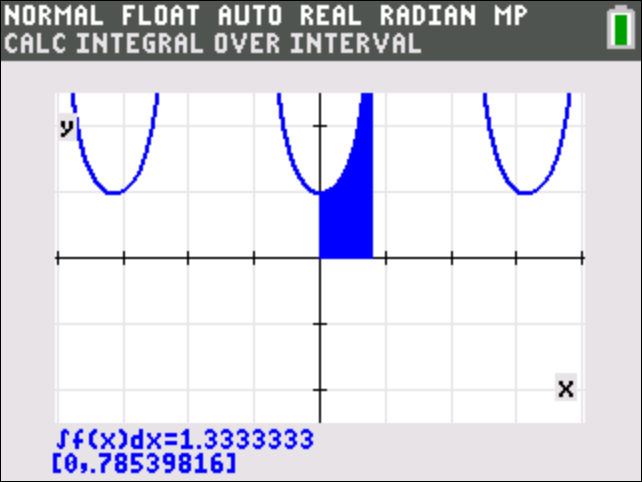
enter image source here

After graphing press 2nd and then TRACE

Press 7 for integration, #intf(x)dx#

Then enter the LOWER and UPPER LIMITS

See the results of those actions below.

enter image source here