What is the derivative of #cos^3(x)#?
1 Answer
Dec 18, 2014
The derivative of
You can get this result using the Chain Rule which is a formula for computing the derivative of the composition of two or more functions in the form:
You can see that the function
Deriving you get:
derivative of
In this case the
First you deal with the cube deriving it but letting the argument
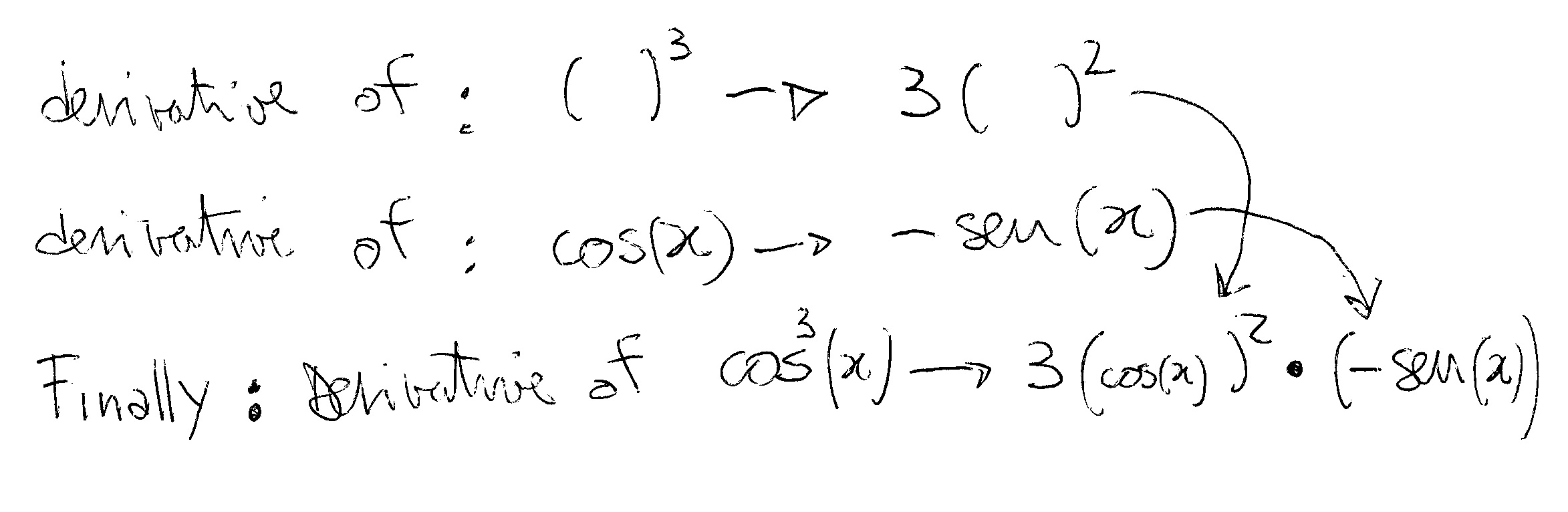
Which is equal to:

