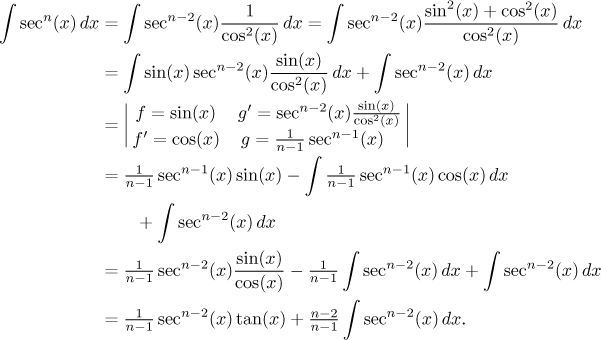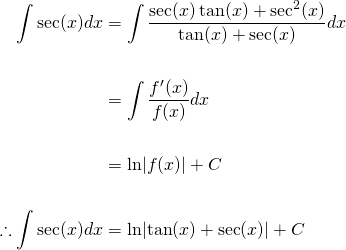#intsec^3(2x)-3sec(2x)dx#
Apply sum rule and take the constant out,
#color(red)(1/2intsec^3(2x)dx)-color(blue)(3/2intsec(2x)dx#
Apply integral reduction (refer to picture 1),
#color(red)(1/2((sec^(3-2)(2x)tan(2x))/(3-1)+(3-2)/(3-1)intsec^(3-2)(2x)))-color(blue)(3/2intsec(2x)dx#
#=color(red)(1/2((sec(2x)tan(2x))/(2)+(1)/(2)intsec(2x)))-color(blue)(3/2intsec(2x)dx#
Integrate #sec# (refer to picture 2),
#color(red)(1/2((sec(2x)tan(2x))/(2)+(1)/(2)ln|tan(2x)+sec(2x)|)-color(blue)(3/2ln|tan(2x)+sec(2x)|#
Simplify,
#color(red)(1/4sec(2x)tan(2x)+(1)/(4)ln|tan(2x)+sec(2x)|)-color(blue)(3/2ln|tan(2x)+sec(2x)|#
#=1/4sec(2x)tan(2x)-5/(4)ln|tan(2x)+sec(2x)|+c#
Reference:
Picture 1: Integral reduction
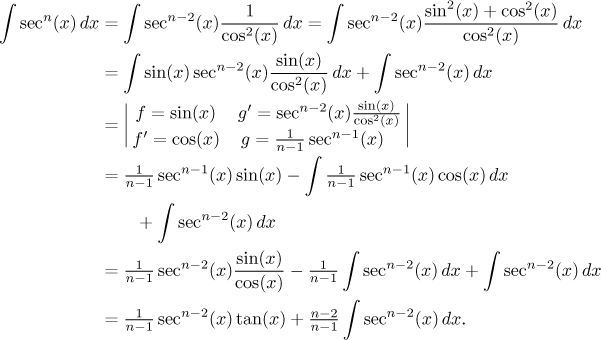
Picture 2: Integral of #secx#
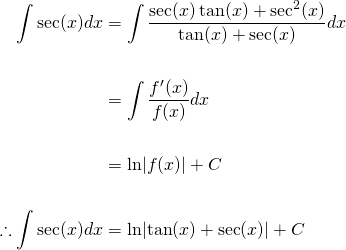
Hope you have a nice day!