What is the derivative of #sin(2x)#?
2 Answers
Jan 25, 2015
I would use the Chain Rule:
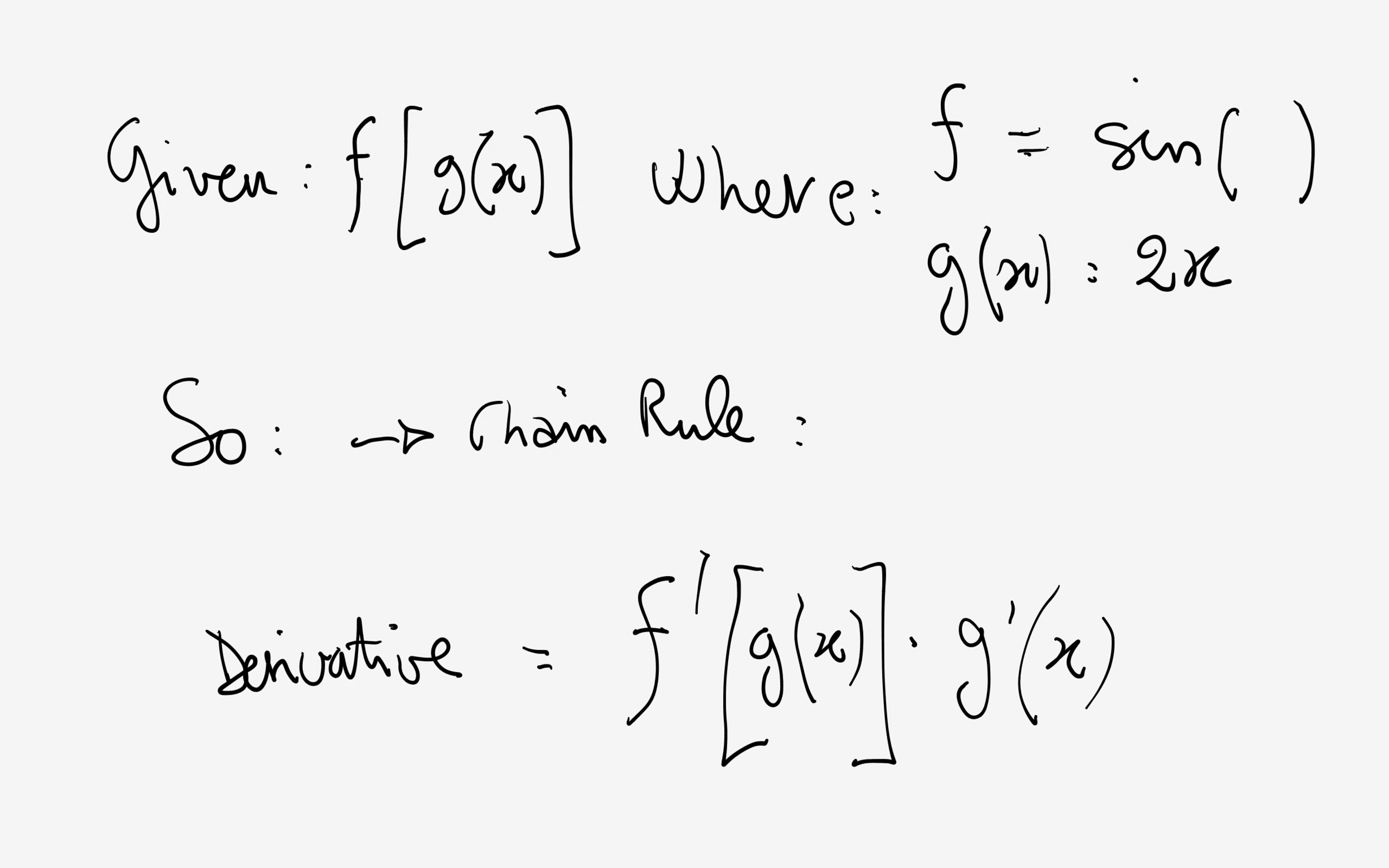
First derive
Jun 20, 2018
Explanation:
The key realization is that we have a composite function, which can be differentiated with the help of the Chain Rule
We essentially have a composite function
We know all of the values we need to plug in, so let's do that. We get
Hope this helps!


