Question

What is the derivative of this function `arcsec(x^3)`?

Answer 1

`=(3x)/sqrt(x^2-1)`

Explanation:

For this you need to know what the derivative of arcsec(x) is.

You can derive it fairly easily:

`y = arcsec(x)`
`sec(y) = x`
`d/dx sec(y) = d/dx x`
`sec(y)tan(y)dy/dx = 1`
`dy/dx = 1/(sec(y)tan(y)`
`dy/dx = 1/(sec(arcsec(x))tan(arcsec(x)))`
`dy/dx = 1/(xsqrt(x^2-1))`

In the last statement I simplified `sec(arcsec(x))` to `x`, which is obvious, but I also simplified `tan(arcsec(x))` to `sqrt(x^2-1)` which is slightly less obvious

If you draw a triangle such that sec(angle) = x, you can understand why it works:

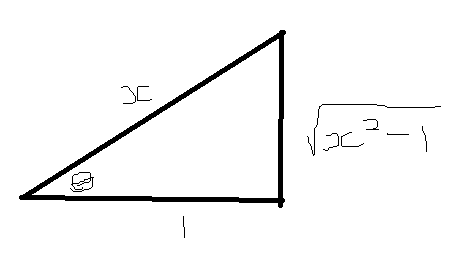
you can see that `arcsec(x) = theta` and `tan(theta) = sqrt(x^2-1)`

`therefore tan(arcsec(x)) = sqrt(x^2-1)`

Now we know the derivative of arcsec(x) and just need to apply a little chainrule to get our answer:

`d/dx arcsec(x^3) = 1/(xsqrt(x^2-1))*d/dx x^3 = (3x^cancel2)/(cancelxsqrt(x^2-1))`
`=(3x)/sqrt(x^2-1)`

Answer 2

`dy/dx = 3/(absxsqrt(x^6-1))`

Explanation:

If `y=arcsec(x^3)` then `secy =x^3`, that is: `cosy=1/x^3`

Differentiate implicitly:

`-sinydy/dx = -3/x^4`

`dy/dx = 3/(x^4siny)`

Now, for `0 <= y <= pi`:

`siny = sqrt(1-cos^2y) = sqrt(1-1/x^6)`

and:

`dy/dx = 3/(x^4 sqrt(1-1/x^6)) = (3sqrt(x^6))/(x^4sqrt(x^6-1))= 3/(absxsqrt(x^6-1))`