What is the difference between vapour pressure of a solvent and vapour pressure of pure solvent in Raoult's law?
1 Answer
The "pure solvent" is the solvent without solute, and the "solvent" (a clearer way is to simply say "solution") is the solvent with solute.
Raoult's law is (Physical Chemistry: A Molecular Approach, Ch. 25-2):
#\mathbf(a_1/chi_1 = P_1/(P_1^"*"chi_1) = gamma_1)# where:
#a_1# is the activity of the solvent. It is like a more accurate concentration.#gamma_1# is the activity coefficient of the solvent. When#gamma_1 = 1# , the solvent is pure.#chi_1# is the mole fraction of the solvent, and is equal to#(n_1)/(n_1 + n_2)# , where#n_2# is#"mol"# s of solute and#n_1# is#"mol"# s of solvent.#P_1# is the vapor pressure of the solvent (solution with solute).#P_1^"*"# is the vapor pressure of the pure solvent (solution without solute).
APPROACHING IMPURITY
Basically, the idea is if you add solute to a solvent, the mole fraction of solvent has decreased because a smaller percentage of the solution belongs to the solvent. So, what I mean is:
#chi_1 = n_1/(n_1 + n_2)#
becomes smaller as
Here's some example data using an equation from my book (Ch. 24) where I add solute to the solution. The solution starts with
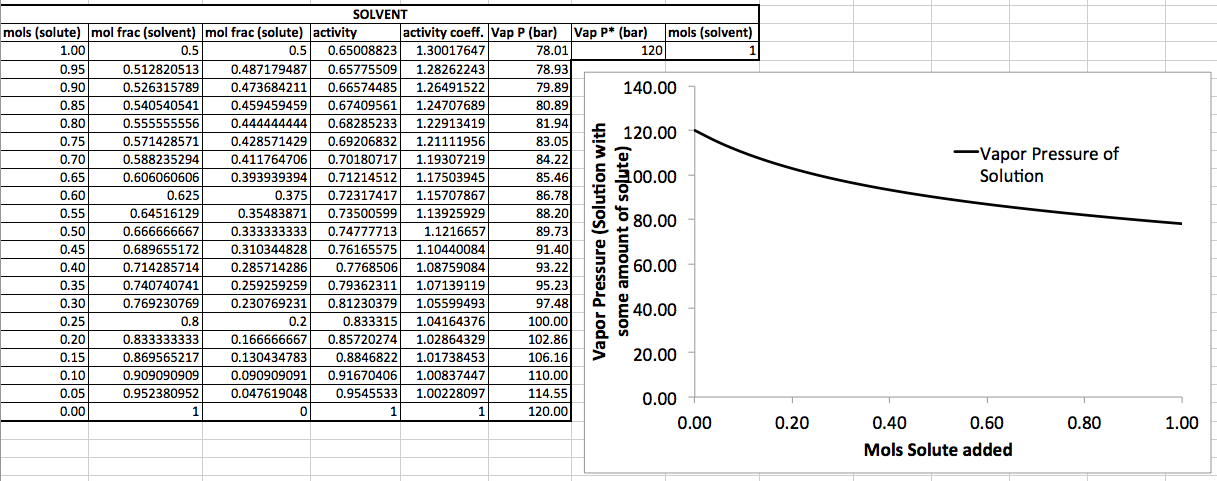
APPROACHING PURITY
Now, let's consider going the other way. That means you go leftwards on the curve.
If you "undissolve" the solute and then take solute out of the solution, it follows that you have decreased
Now, go all the way until
Note the following relationship derived from Raoult's law:
#gamma_1 = a_1/chi_1#
Based on what we just said, it follows that
When
#\mathbf(chi_1 = 1)# ,#\mathbf(P_1 = P_1^"*")# .
That means the vapor pressure of the impure solvent and that of the pure solvent are equal. The only way that could be true is if there is no solute in solution, which makes sense because we've been removing the solute!
Thus, with no solute, the concentration of pure solvent to solution is
So, the gist of it is that:
#P_1# is the vapor pressure of the solvent for when#chi_1 < 1# and#a_1 < 1# . This means you have an impure solution (with solute in the solvent).#P_1^"*"# is the vapor pressure for the solvent when#chi_1 = a_1 = gamma_1 = 1# . Thus,#P_1 = P_1^"*"# for a pure solution (no solute in the solvent).

