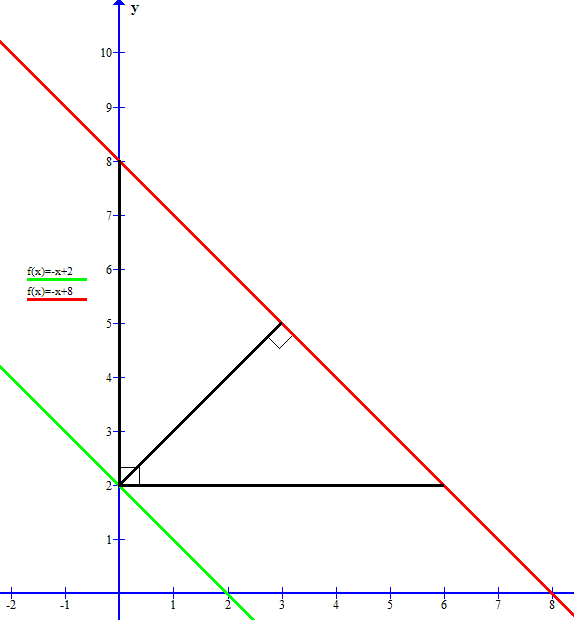
What is the distance between parallel lines whose equations are y=-x+2 and y=-x+8?
1 Answer
Distance:
Explanation:
Giving us the points
The vertical distance between the two lines is the vertical distance between
The horizontal distance between the two lines is the horizontal distance between
Consider the triangle formed by these
The length of the hypotenuse (based on the Pythagorean Theorem) is
The area of the triangle using the horizontal vertical sides is
But we can also get this area using the perpendicular distance from the hypotenuse (let's call this distance
Note that
#"Area"_triangle = 1/2 * 6sqrt(2) * d " sq.units
Combining our two equations for the area gives us