What is the distance between the following polar coordinates?: # (1,(-23pi)/12), (3,(5pi)/8) #
1 Answer
Jun 12, 2017
The distance,
Explanation:
When given two polar points
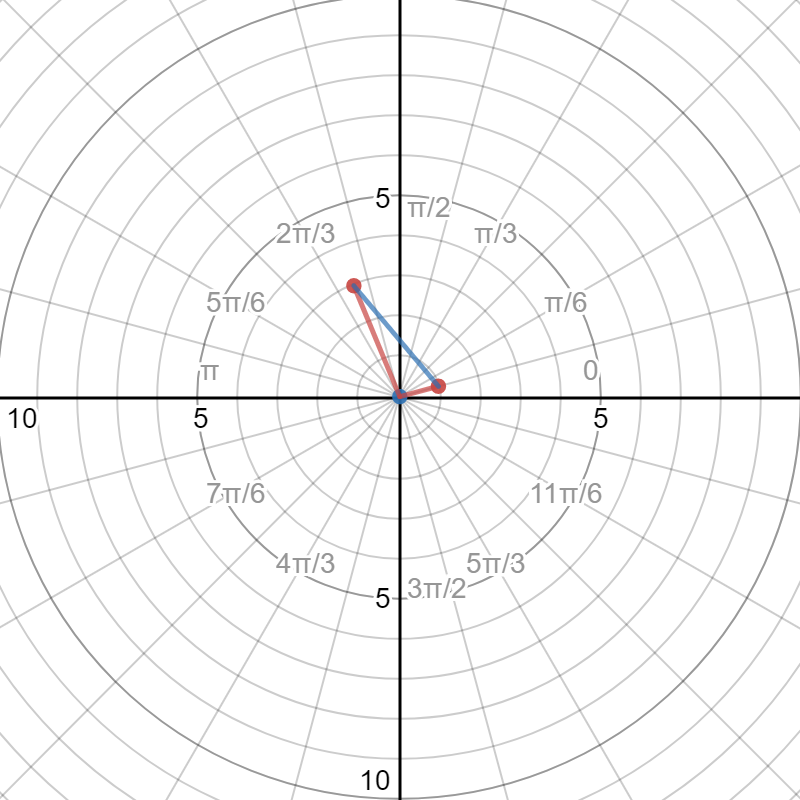
We can use the Law of Cosines to find the length, c, of the blue line:
Using the two given points we assign:
Substituting into equation [1]:
