What is the distance between the following polar coordinates?: # (2,(pi)/8), (7,(3pi)/8) #

Question

970 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-09T12:14:53

# sqrt( 53 - 14sqrt 2 ) #

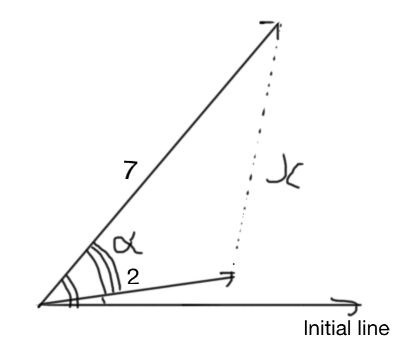
enter image source here

As scene of the picture, i have drawn each of the polar coordinates, with there respective lengths and angles

We can see that #alpha = (3pi)/8 - pi/8 = pi/4 #

Now we can use the cosine rule to find #x# our distance:

#A^2 = B^2 + C^2 -2BCcosa#

# => x^2 = 7^2 + 2^2 - (2*7*2*cos(pi/4))#

#=> x^2 = 53 - 14sqrt2 #

As #cos(pi/4) = sqrt2 /2 #

Hence yielding:

# sqrt( 53 - 14sqrt 2 ) #