Let's solve a general case; say we have two points of Polar coordinates #A(r_1,varphi_1)# and #B(r_2,varphi_2)#. Let us visualise the situation:
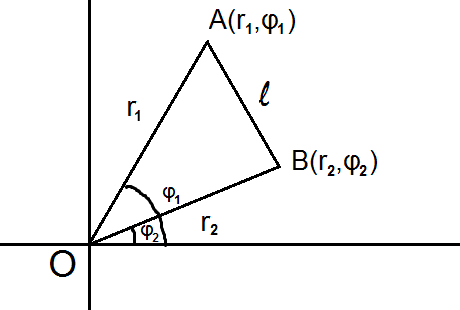
Let #l# be the distance between #A# and #B#:
#l = AB#
We might convert #A# and #B# to Cartesian coordinates, for which we have a formula, but instead let's keep everything in Polar.
In the triangle #DeltaAOB#, we know the lenght of the sides #OA#, #OB# and the angle between the; #/_ AOB#.
As such, we can apply the cosine law:
#AB^2=OA^2+OB^2-2OA*OBcos(/_AOB)#
Substituting everything into Polar coordinates:
#l^2=r_1^2+r_2^2-2r_1r_2cos(varphi_1-varphi_2)#
Finally, we can solve our particular case:
#A(-4,(3pi)/4) and B(5,(3pi)/8)#
#:. l^2 =(-4)^2+5^2-2(-4)*5cos((3pi)/4-(3pi)/8)#
#:. l^2 = 16+25+40cos((3pi)/4)#
Notice how #(3pi)/4=pi-pi/4#, hence
#cos((3pi)/4) = -cos(pi/4)=-sqrt2/2#
#:. l^2=41-40*sqrt2/2=41-20sqrt2#
#:. l =sqrt(41-20sqrt2)#

