What is the distance between the following polar coordinates?: # (4,pi), (5,pi) #
2 Answers
Explanation:
The distance formula for polar coordinates is
Where
Let
Hence the distance between the given points is
Explanation:
(this is an attempt to restore my original answer)
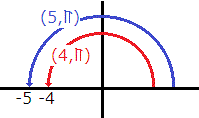
Using common insight rather than applying the Pythagorean Theorem and
The distance between any two polar coordinates with the same angle is the difference in their radii.


