Before finding the distance between these points, it is necessary to convert them to rectangular coordinates. These points have been plotted as in the given figure and explained as follows:
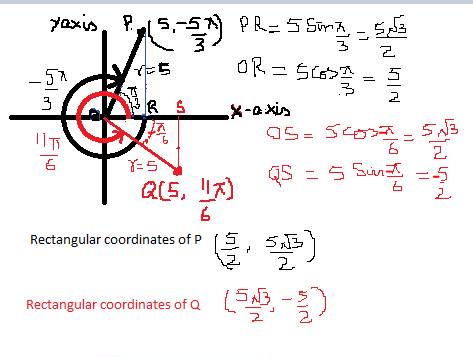
To plot the point #(5, (-5pi)/3)#,go #(5pi)/3# radians or #300^o# clockwise from x- axis and mark point P at a radial distance of 5 units from the origin O. This is shown in the black pen. Now draw a perpendicular PR from point P to the x -axis. In the right triangle POR, #angle#POR is #pi/3#. OR=5 cos#pi/3= 5/2# and PR= 5 sin#pi/3= (5sqrt3) /2#. Thus rectangular coordinates of P are #(5/2, (5sqrt3)/2)#
To plot the point #(5, (11pi)/6)#, go #(11pi)/6# or #330^o# counterclockwise from x -axis and mark point Q at a radial distance of 5 units from the origin O. This is shown in red pen. Now draw a perpendicular QS from point Q to the x -axis. In the right triangle QOS, #angle# QOS is #(-pi)/6#. OS =#5 cos(-pi/6)= (5sqrt3)/2# and QS= 5sin#(-pi)/6 = -5/2# Thus rectangular coordinates of Q are #((5sqrt3)/2, -5/2)#
Distance between points P and Q= #sqrt( (5/2-(5sqrt3)/2)^2 +((5sqrt3)/2 +5/2)^2)#
=#sqrt(2(25/4 +75/4)#
= 5#sqrt2#

