#" "#
#color(green)"Step 1:"#
Domain:
The domain of the given function #f(x)# is the set of input values for which #f(x)# is real and defined.
Point to note:
#color(red)(sqrt(f(x)) = f(x)>=0#
Solve for #(x-1)>=0# to obtain #x>=1#.
Hence,
#color(blue)("Domain: " x>=1#
Interval Notation: #color(brown)([1, oo)#
#color(green)"Step 2:"#
Range:
Range is the set of values of the dependent variable used in the function #f(x)# for which #f(x)# is defined.
Hence,
#color(blue)("Range: " f(x)>=0#
Interval Notation: #color(brown)([0, oo)#
#color(green)"Step 3:"#
Additional note:
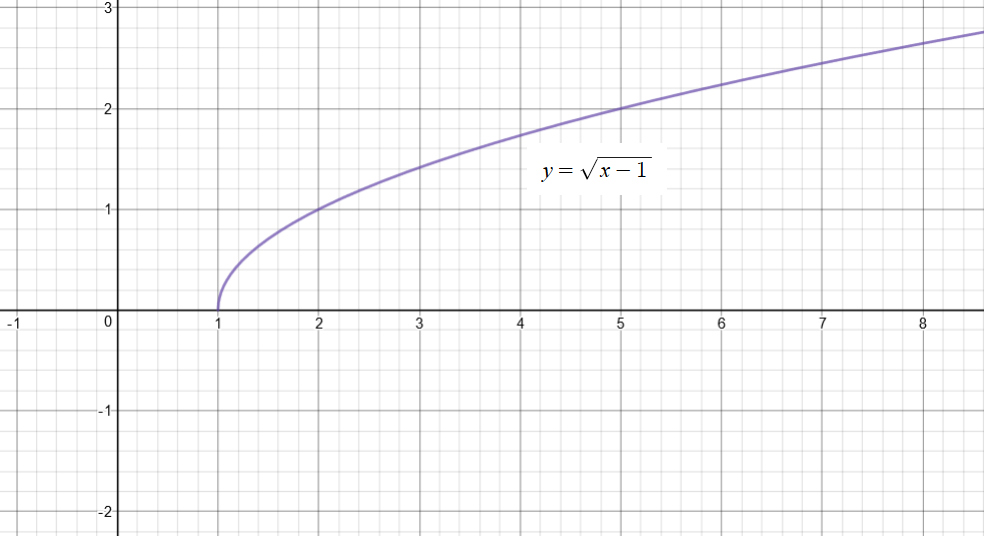
The function #y = f(x)= sqrt(x-1)# has no asymptotes.
Create a data table using values for #x# and corresponding values for #y#:
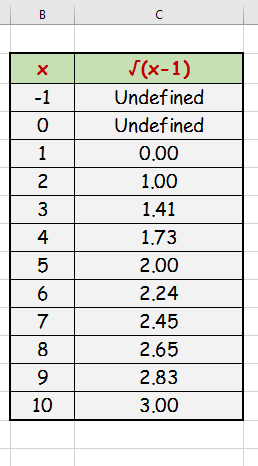
Observe that #Zero# and #"Negative values"# of #x# make the function #f(x)# #"undefined"# at those points.
Graph #f(x) = sqrt(x-1# to verify the results obtained: