What is the domain and range of the function # f(x)=5/x#?
2 Answers
The domain is
The range is
Explanation:
In general, we start with the real numbers and then exclude numbers for various reasons (can't divide by zero and taking even roots of negative numbers being the main culprits).
In this case we cannot have the denominator be zero, so we know that
A better notation is
For the range, we use the fact that this is a transformation of a well known graph. Since there are no solutions to
Domain :
Range :
Refer to the graph attached to examine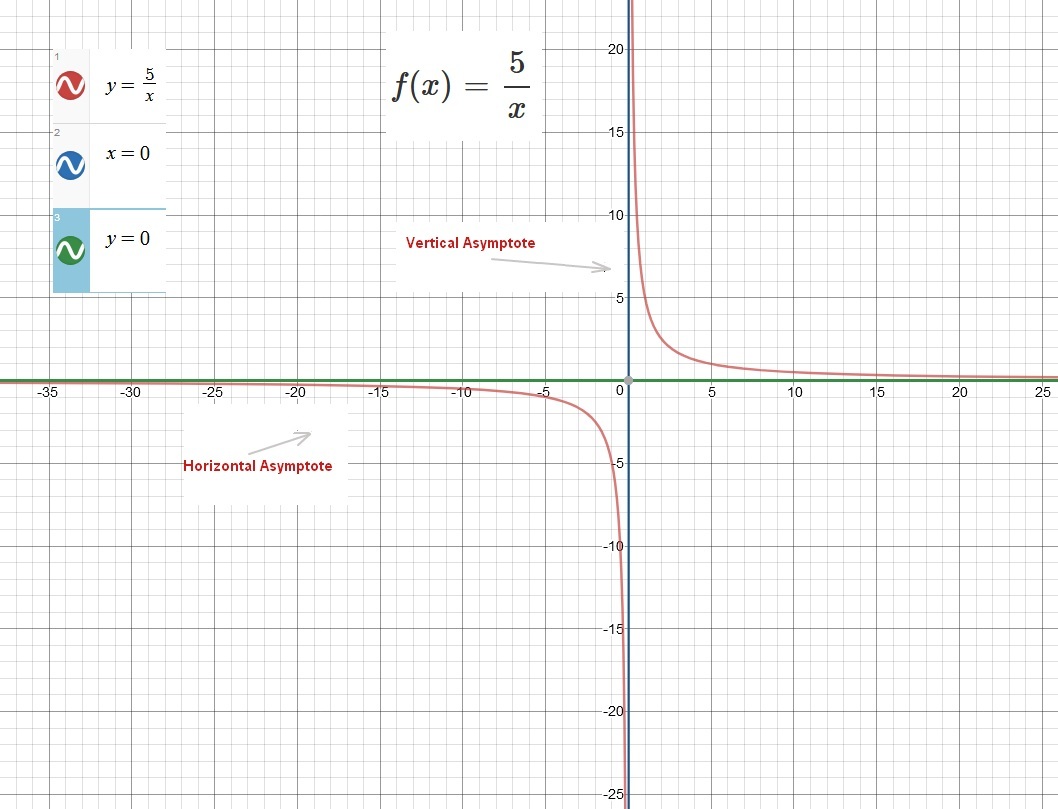 the rational function and the curve's asymptotic behavior.
the rational function and the curve's asymptotic behavior.
Explanation:
A Rational Function is a function of the form
The Domain :
When dealing with the Domain of a Rational Function, we need to locate any points of discontinuity .
As these are the points where the function is not defined, we simply set
In our problem, at
Hence, our Domain :
Using interval notation :
We can also write our Domain :
That is to say the Domain includes all Real Numbers except x = 0.
Our function will continuously approach our asymptote but never quite reach that.
The Range :
To find the Range, let us make x as the subject of our function.
We will start with
Multiply both sides by x to get
Like we did for the domain , we will find out for what value(s) of y does the function is undefined.
We see that it is
Hence, our Range :
Please refer to the graph attached for a visual representation of our rational function and it's asymptotic behavior.


