Question

What is the domain and range of `y= (-2^-x) - 4`?

Answer 1

Domain is `-oo < x < +oo`

Using Interval Notations we can write our domain as

`(-oo, +oo)`

Range: `f(x) < -4`

`(-oo,-4)` using Interval Notations

Explanation:

We have the function `f(x) = [-2 ^ (-x) ] - 4`

This function can be written as

`f(x) = [-1/2 ^ x ] - 4`

Please analyze the graph given below:

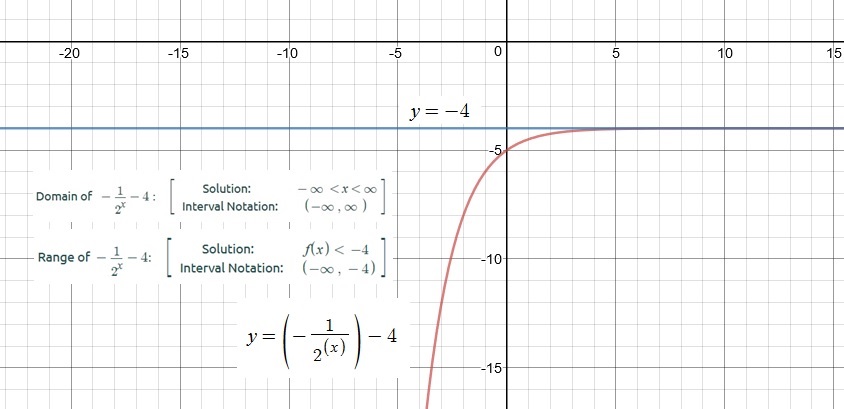
Domain:

The domain of a function f(x) is the set of all values for which the function is defined.

We observe that the function does not have any undefined points.

The function does not have any domain constraints either.

Hence, domain is `-oo < x < +oo`

Using Interval Notation we can write our domain as `(-oo, +oo)`

Range:

The range of the function is the set of all values that `f(x)` takes.

From our graph, we observe that the range* is `f(x)<-4`

Using Interval Notations we can write our range as

`(-oo,-4)`

Additional note:

It is useful to remember that the range of the function is same as the domain of the inverse function.