What is the energy of an electron in the hydrogen atom determined by?
2 Answers
Observation of light emitted (photons) when the atom 'relaxes' from and excited state back to its ground state.
Explanation:
The related experiments also verified the concept of "quantum states" - NO, that term does not mean "huge", as often misrepresented! It means a particular, discrete amount (actually often miniscule).
We can put just about any level of energy from any source into an atom (hydrogen, in this case), and excite its electrons from their normal stable orbits (energy levels) to higher ones.
It is observed that no matter what energy levels are put in , ONLY certain energy levels are observed in the relaxation (or none, if the energy was insufficient to excite even the first electron). That is the energy release from an electron moving from a higher to a lower (stable) energy level.
http://hyperphysics.phy-astr.gsu.edu/hbase/hyde.html
http://iopscience.iop.org/article/10.1088/0022-3700/3/2/018/pdf
http://venables.asu.edu/quant/Dinesh/Bohratom2.html
The energy of a hydrogen atom's electron is determined by which principal quantum number
In atomic units, the hydrogen one-electron energy
#E_n = -"13.61 eV" cdot 1/n^2# where
#n = 1, 2, 3, . . . # is the quantum number that quantizes the energy levels. That is, they are discrete energy values proportional to#1/n^2# . [There are#1.602 xx 10^(-19) "J"# in#"1 eV"# .]
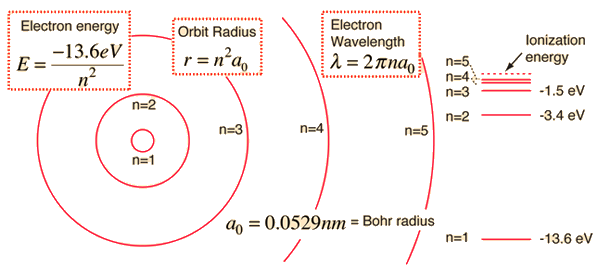
And one can shift the electron to different energy levels. Commonly:
-
Input of light energy
#hnu# excites the electron to higher energy states, i.e.#Deltan > 0# . -
Emission of light energy
#hnu# occurs when the excited electron relaxes to lower energy states, i.e.#Deltan < 0# .
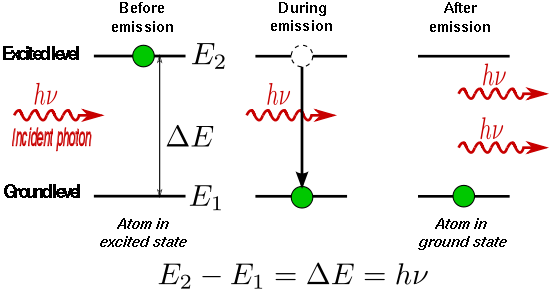
An electron cannot land on an "intermediate" energy state where
It also is not localized outside the atom, where the energy levels become classical, or continuous. Instead, it just cannot be found outside the atom.


