Question

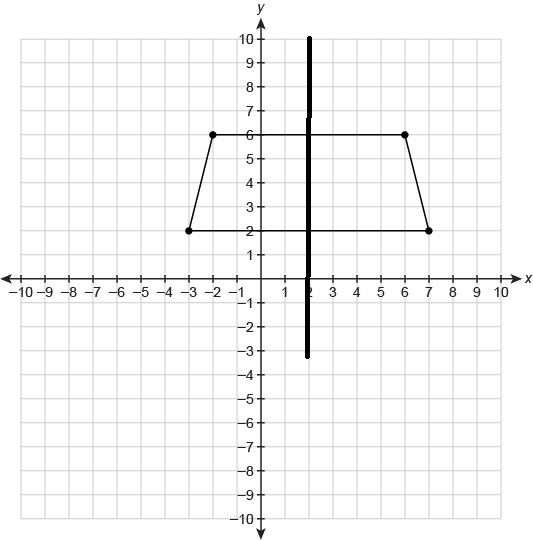
What is the equation for the line of reflection that maps the trapezoid onto itself?

Answer 1

The equation of line of reflection is `x=2`

Explanation:

It is apparent that we can have a line of reflection that maps a trapezoid onto itself,

1. only when the trapezoid has the two non-parallel sides are equal in length and angles they make with any of the parallel sides too are equal (in fact the first condition in a trapezium leads to second) i.e. an isosceles trapezoid. Here, it is so and hence we have a line of reflection that maps a trapezoid onto itself.

2. Further such a line of reflection would be perpendicular to the parallel sides and as here parallel sides are parallel to `x`-axis, the line of reflection would be parallel to `y` axis i.e. of the form `x=a`

3. Further as every point and its reflection is equidistant from the line of reflection, the line of reflection must pass through the midpoints of parallel sides.

4. In the given figure, mid points of parallel sides are `(2,2)` and `(2,6)`

Hence the equation of line of reflection is `x=2` and appears as thick line shown in figure below.