What is the equation in standard form of the parabola with a focus at (14,-19) and a directrix of y= -4?
1 Answer
Jul 7, 2018
(x−14)2=30(y+11.5)
Explanation:
Given -
Focus
Directrix
Find the equation of the parabola.
Look at the graph.
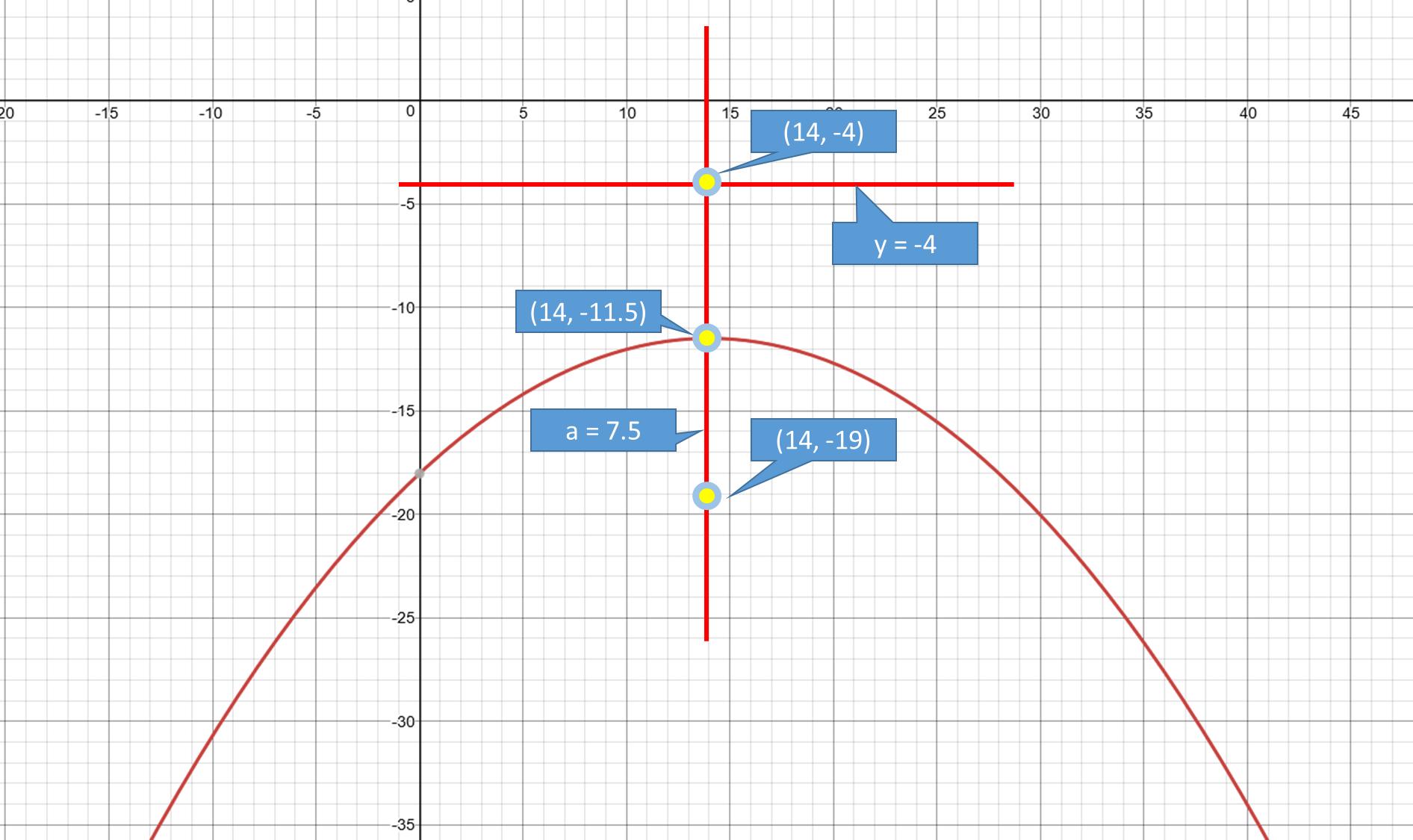
From the given information, we can understand the parabola is facing downward.
The vertex is equidistance from directrix and focus.
Total distance between the two is 15 units.
Half of 15 units is 7.5 units.
This is
By moving down 7.5 units down from
Hence vertex is
The vertex is not at the origin. Then, the formula is
(x−h)2=4a(y−k)
Plug in the values.
(x−14)2=4(7.5)(y+11.5)
(x−14)2=30(y+11.5)

