What is the equation in standard form of the parabola with a focus at (21,15) and a directrix of y= -6?
1 Answer
Jun 15, 2018
#(x-21)^2=42(y-4.5)#
Explanation:
Given -
Focus
Directrix
This parabola opens up. Its origin is away from the origin
Where -
#h=21#
#k=4.5#
#a=10.5#
Look at the graph
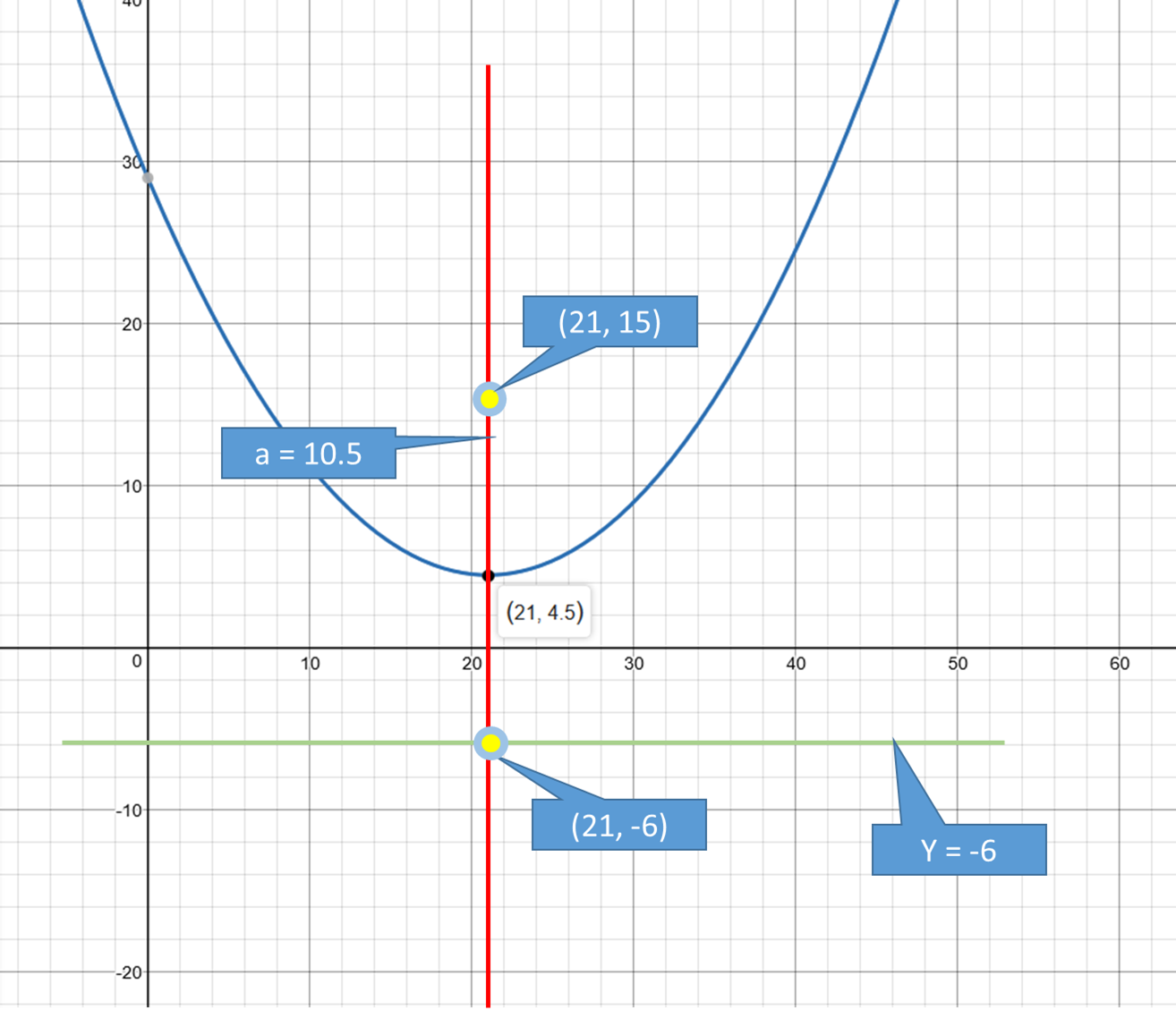
Hence the general form of the equation is -
#(x-h)^2 = (4)(a)(x-k)#
#x-21)^2=(4)(10.5)(y-4.5)#
#(x-21)^2=42(y-4.5)#

