Question

What is the equation of the circle which touches the y-axis at ( 0 , 3 ) and passes through ( 1 , 0 )?

Answer 1

`(x-5)^2+(y-3)^2=25`

Explanation:

If the circle is tangent to the Y-axis at `(0,3)` then its center is along the line `y=3`.
If it passes through the point `(1,0)` then its center is in Quadrant I at some point `(x_c,3)` and its radius is `x_c`

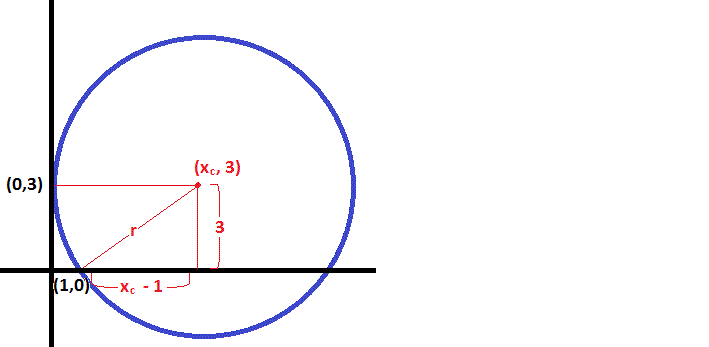
By the Pythagorean Theorem, the square of its radius is
`color(white)("XXX")r^2=x_c^2=3^3+(x_c-1)^2`

Simplifying we have
`color(white)("XXX")cancel(x_c^2) = 9+ cancel(x_c^2) -2x_c+1`
or
`color(white)("XXX")r=x_c=5`

Using the general standard formula for a circle with radius `r` and center `(a,b)`:
`color(white)("XXX")(x-a)^2+(y-b)^2=r^2`
and substituting `(a,b)=(5,3)` for the center and `r=5` for the radius:
`color(white)("XXX")(x-5)^2+(y-3)^2=25`