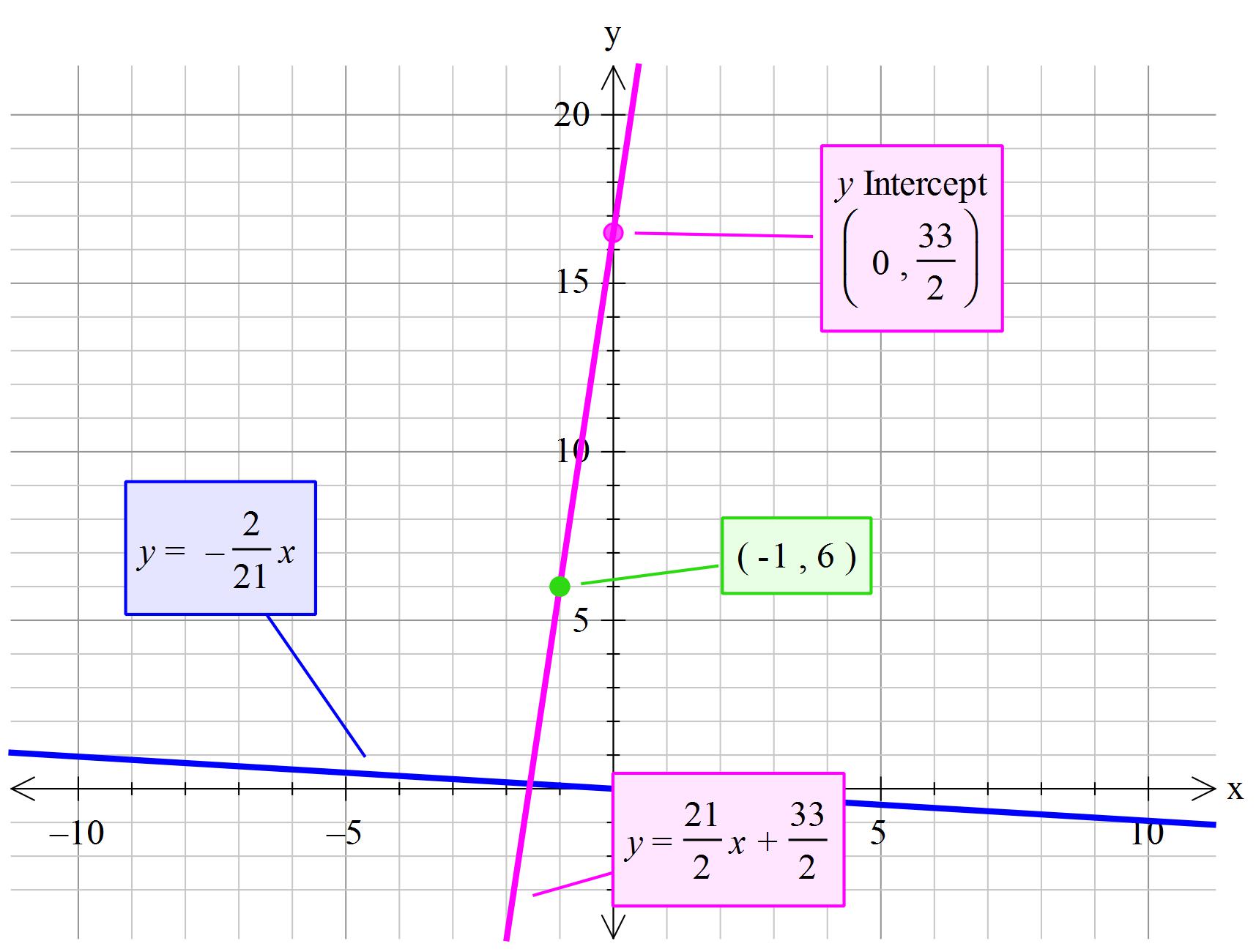
What is the equation of the line perpendicular to #y=-2/21x # that passes through # (-1,6) #?
2 Answers
The slope of a perpendicular line is the negative reciprocal of the original line.
Explanation:
The slope of the perpendicular line is
Now we can use point slope form to plug in the point, the slope abs find the slope intercept form equation.
The point (-1,6) is
Hopefully this helps!
Explanation:
Given:
Compare to the standard form of
Where
In your equation
If
'~~~~~~~~~~~~~~~~~~~~~~~~~~~
We know that this new line passes through
So substitute into equation (2) the values
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The line perpendicular to that given is: