Question

What is the equation of the line perpendicular to `y=6x` that passes through `(6,-1)`?

Answer 1

Different way of saying the same thing:

`color(blue)(y=-1/6x)`

Explanation:

`color(blue)("General Introduction")`

Given:`" "y=6x`

Compare to the standard equation form of `y=mx+c`
Where `m` is the gradient (slope)

Looking at the question we see that the gradient is 6.
This means that for 1 along on the x-axis the line has gone up 6 on the y-axis.

`color(blue)(y=6x" "->" gradient "->" "m=6)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(white)(.)`

`color(blue)("Building the equation of the perpendicular line")`

`color(brown)("A line perpendicular to "y=mx+c" has gradient "-1/m`

If `m=6" then "-1/m=-1/6`

So the straight line perpendicular to that given has the equation

`color(blue)(y=-1/mx+c" "->" " y=-1/6x+c)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(white)(.)`
`color(blue)("Determine the value of the constant "c)`

This line passes through the point `(x,y)->(6,-1)`

So by substitution

`y=-1/6x+c" "->" "-1=-1/(cancel(6))(cancel(6))+c`

`=>c=0`

so the equation of the perpendicular line is:

`color(blue)(y=-1/6x)`

Answer 2

`y = -1/6x`

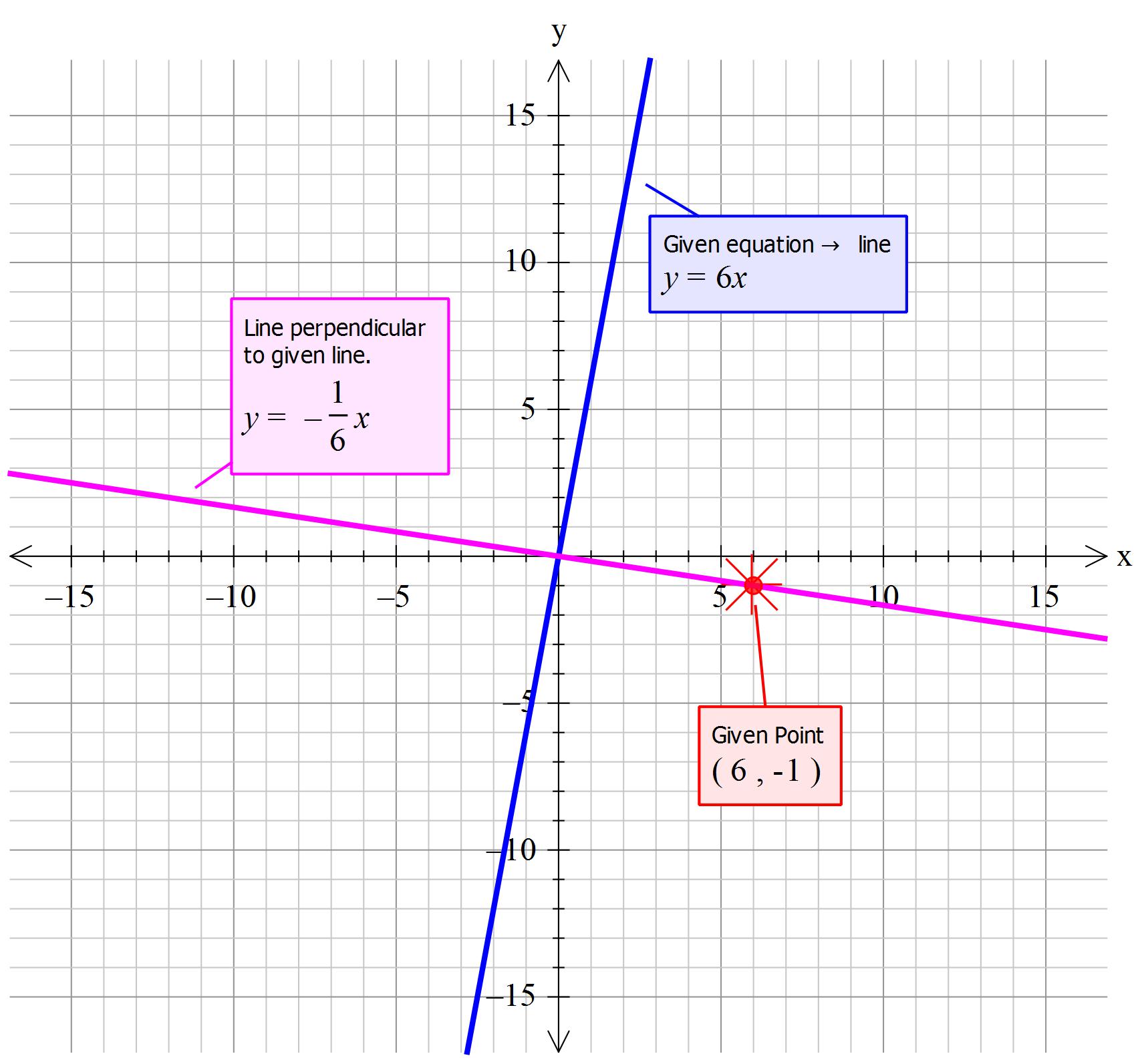
Explanation:

When lines are perpendicular, one slope is the negative reciprocal of the other.
In `y = 6x` the gradient is 6.

The slope perpendicular to this is `-1/6`

We now have the slope and the point `(6,-1)`

There is really nifty formula which applies in a case like this. We have the slope and one point and need to find the equation of the line.

`(y- y_1) = m(x-x_1)` where the given point is `(x_1,y_1)`

Substitute the values given.

`y-(-1) = -1/6(x-6)" "` multiply out and simplify.

`y +1 = -1/6x +1`

`y = -1/6x`