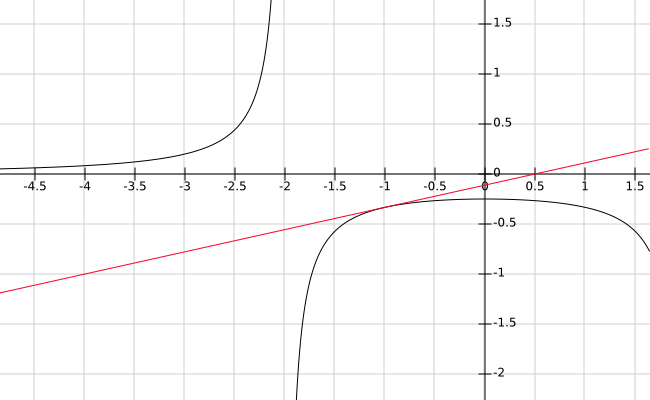
What is the equation of the line tangent to # f(x)=1/(x^2-4) # at # x=-1 #?

Question

2748 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-12T16:25:09

The equation of the tangent line is:

#y(x) = 2/9x -1/9#

The equation of a line tangent to the curve #y=f(x)# in #x = bar x# is given by:

#y(x) = f(barx)+f'(barx)(x-barx)#

We have:

#f(x) =1/(x^2-4)#

#f'(x) = (-2x)/((x^2-4)^2)#

For #barx =-1#

#f(-1) =1/((-1)^2-4) = -1/3#

#f'(-1) = (-2(-1))/(((-1)^2-4)^2)=2/9#

So that the equation of the tangent line is:

#y(x) = -1/3+2/9(x+1) = 2/9x -1/9#

enter image source here