Question

What is the equation of the line tangent to `f(x)=(-3x-1)/(x+4)` at `x=-2`?

Answer 1

Tangent Line is

`11x+4y=-12`

Explanation:

Given equation `f(x)=(-3x-1)/(x+4)` at the point `x=-2`

Let us solve the point `(x_1, y_1)`
Let `x_1=-2`

Using `y=(-3x-1)/(x+4)`

`y_1=(-3x_1-1)/(x_1+4)`

`y_1=(-3(-2)-1)/(-2+4)`

`y_1=5/2`

We have `(x_1, y_1)=(-2, 5/2)`

Let us solve the slope `m`

`m=f' (x)` at `x=x_1=-2`

`m=d/dx((-3x-1)/(x+4))`

`m=((x+4)*d/dx(-3x-1)-(-3x-1)*d/dx(x+4))/(x+4)^2`

`m=((x+4)*(-3)-(-3x-1)*1)/(x+4)^2`

`m=((-2+4)*(-3)-(-3(-2)-1)*1)/(-2+4)^2`

`m=((2)*(-3)-(6-1)*1)/(2)^2`

`m=-11/4`

Let us solve the tangent line

`y-y_1=m(x-x_1)`

`y-5/2=(-11)/4(x--2)`

`y-5/2=(-11)/4(x+2)`

`4y-10=(-11)(x+2)`

`4y=(-11)(x+2)+10`

`4y=-11x-22+10`

`11x+4y=-12`

Kindly see the graph of `f(x)=(-3x-1)/(x+4)` and `11x+4y=-12`

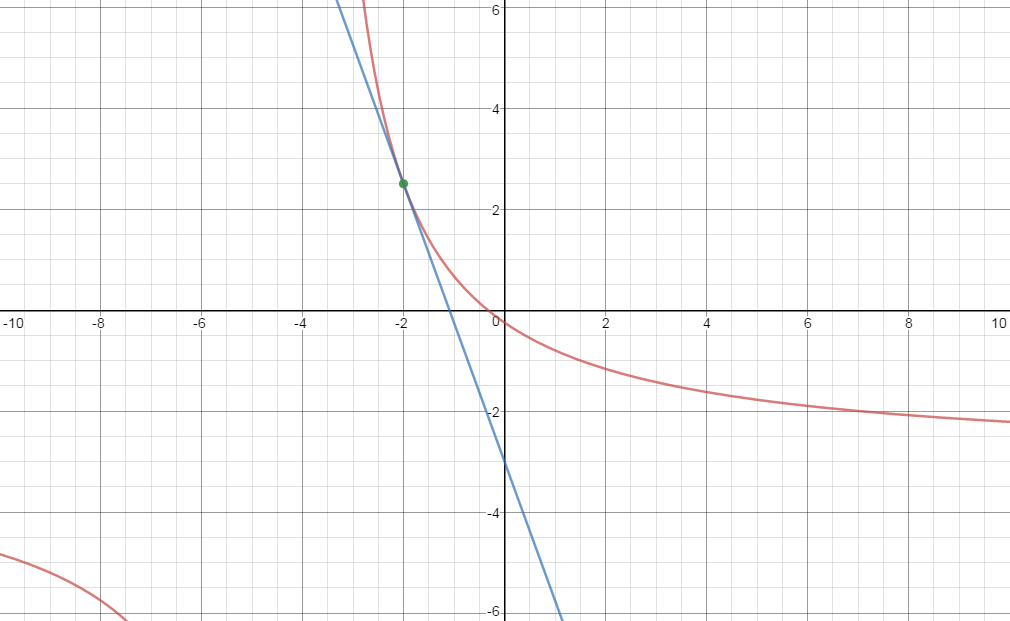
God bless....I hope the explanation is useful.