Question

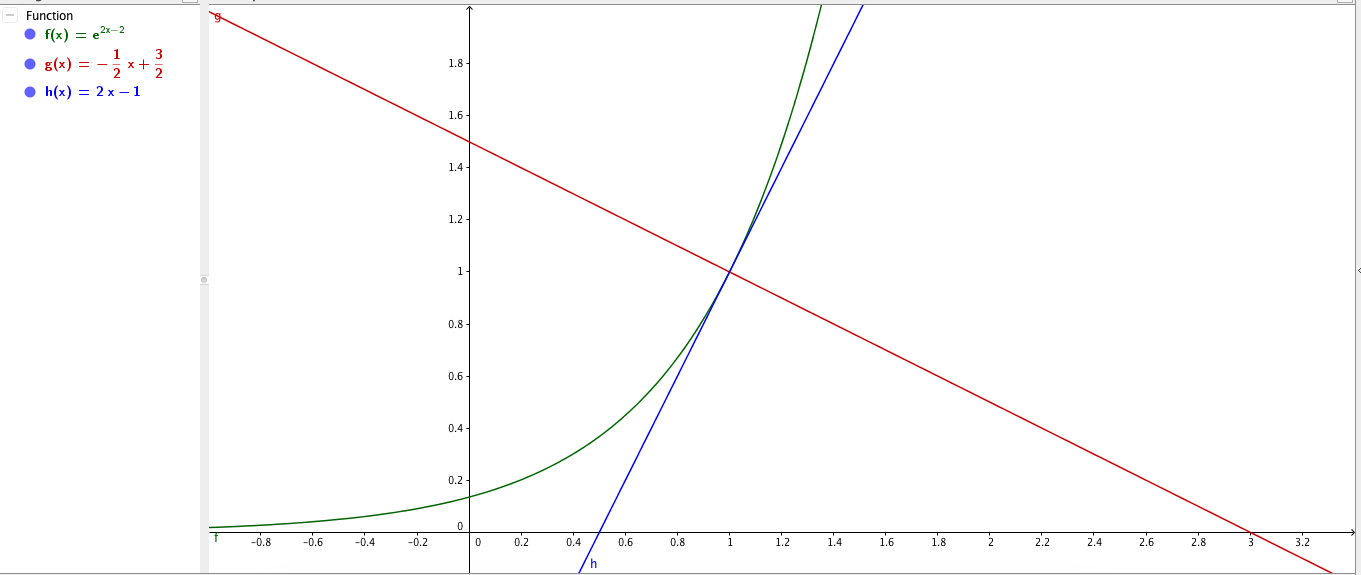
What is the equation of the line that is normal to `f(x)= e^(2x-2)` at `x= 1`?

Answer 1

It is `y=-1/2x+3/2`.

Explanation:

We can first find the tangent to that curve in the point `x=1`.
The slope of the tangent is given by the derivative

`m_t=d/dxe^(2x-2)` when `x=1`

`m_t=e^(2x-2)*d/dx(2x-2)=2e^(2x-2)` and when `x=1` it is

`m_t=2e^2-2=2*e^0=2`.

This is the slope of the tangent line. The normal line is orthogonal to this line. The slope of the orthogonal line is `m_n=-1/m_t=-1/2`.
Then the normal has slope `-1/2`.
The equation of the line is

`y=-1/2x+q` and we have to find `q`. To do this we impose the passage from the point `x=1` and we have to evaluate the `y` calculating `y=e^(2x-2)=e^(2*1-2)=e^0=1`. Then the line passes for the point `(1,1)`.

I substitute this in the equation of the normal line

`y=-1/2x+q`

`1=-1/2*1+q`

`q=1+1/2=3/2`

Then the equation of the normal is

`y=-1/2x+3/2`.