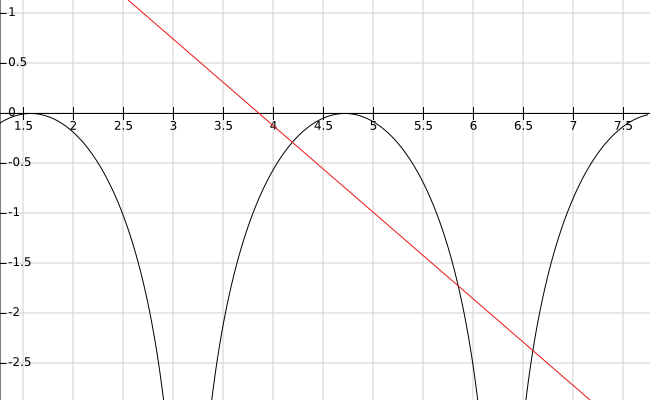
What is the equation of the line that is normal to #f(x)= ln(sin^2x) # at # x=(4pi)/3 #?
1 Answer
Dec 28, 2016
Explanation:
The equation of the line normal to the curve
In our case:
and
So the normal line is: