First we need to differentiate the function in order to find the gradient at #x=2#.
If we rewrite #x/(sqrt(2x+2))# as #x*(2x+2)^(-1/2)# we can use the product rule and the chain rule.
The product rule:
#dy/dx (a*b)= b*(da)/dx + a*(db)/dx#
#d/dx(x)=1#
#d/dx(2x+2)^(-1/2)=-1/2(2x+2)^(-3/2)*(2)=-(2x+2)^(-3/2)#
#dy/dxx*(2x+2)^(-1/2)=(2x+2)^(-1/2) +x * (-(2x+2)^(-3/2))#
#->(1)/((2x+2)^(1/2))-(x)/(2x+2)^(3/2)=((2x+2)-x)/((2x+2)^(3/2))=(x+2)/((2x+2)^(3/2))=(x+2)/((2x+2)(2x+2)^(1/2))=1/2(x+2)/((x+1)sqrt(2x+2)#
#f^'(x)=1/2(x+2)/((x+1)sqrt(2x+2)#
Gradient at #x=2#
#1/2(2+2)/((2+1)sqrt(2(2)+2))=4/(6sqrt(6))=sqrt(6)/9#
For the normal line:
#sqrt(6)/9=-(3sqrt(6))/2#
Point on the line:
Plugging 2 into original function:
#2/(sqrt(2(2)+2))=2/(sqrt(6))=(sqrt(6))/3#
#(2color(white)(8) , (sqrt(6))/3)#
#y-(sqrt(6))/3=-(3sqrt(6))/2(x-2)#
#->y=-(3sqrt(6))/2x+(6sqrt(6))/2+(sqrt(6))/3=-(3sqrt(6))/2x+(10sqrt(6))/3#
Normal line:
#y==-(3sqrt(6))/2x+(10sqrt(6))/3#
Or:
#6y=-9sqrt(6)*x+20sqrt(6)#
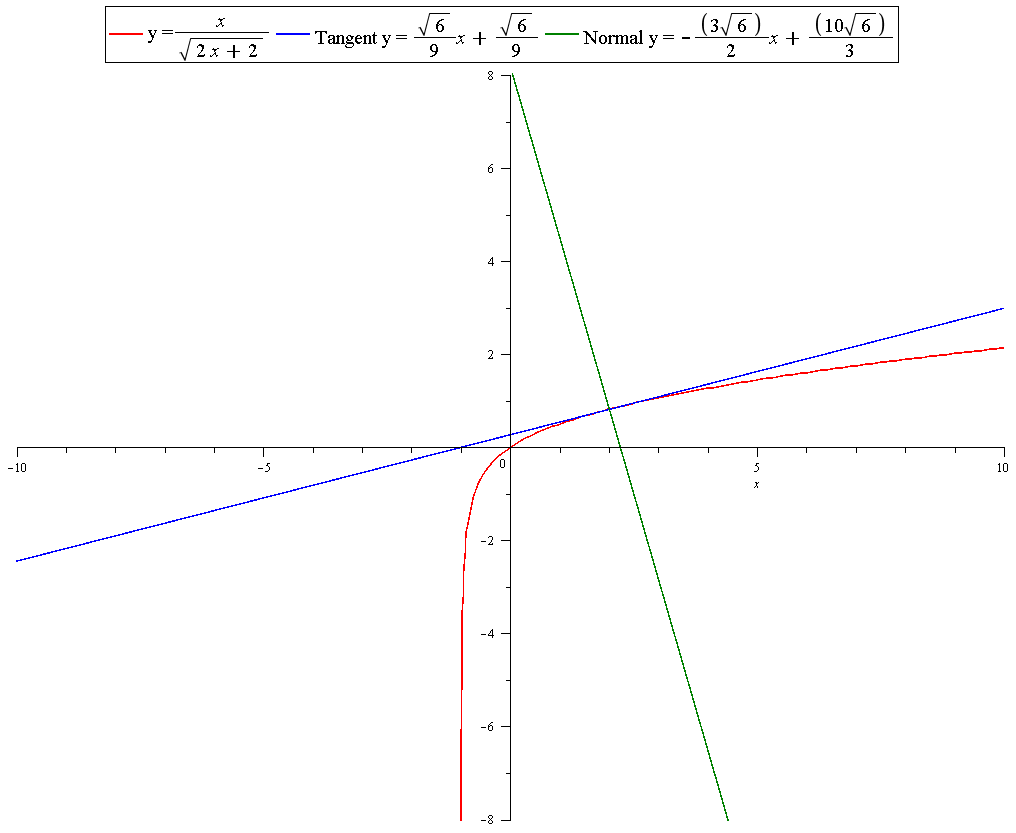
Plot: