Question

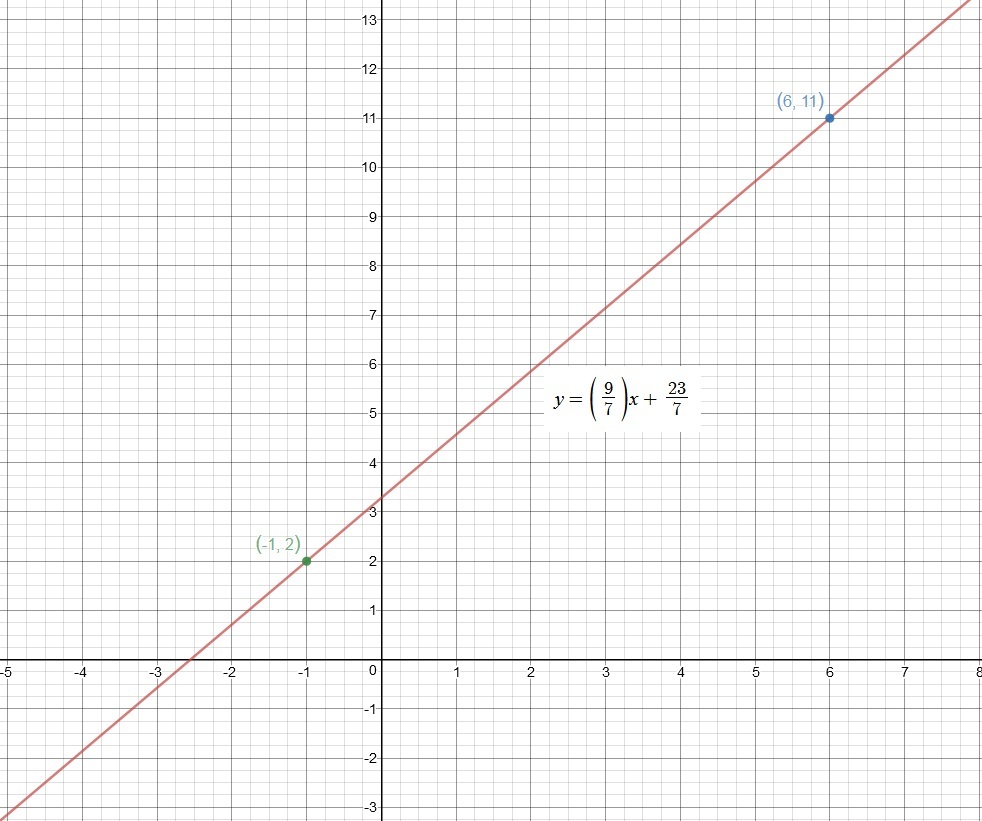
What is the equation of the line that passes through (6,11) ,( - 1,2)?

Answer 1

`color(blue)(y=9/7x+23/7)`

Explanation:

We are given two points : -

`color(red)((6, 11), (-1, 2)` .... Points

Let, `color(green)(x_1 = 6 and y_1 = 11)`

Let, `color(green)(x_2 = -1 and y_2 = 2)`

Hence, the two points given to us can be written as

`color(red)((x_1, y_1), (x_2, y_2)` .... Points

We will next find the Slope using the formula:

`color(green)(Slope(m) = (y_2 - y_1)/(x_2-x_1))`

`rArr Slope(m) = ( 2- 11)/(-1--6)`

`rArr (-9)/(-7) = 9/7`

Therefore,

`Slope(m) = 9/7`

The Point-Slope Equation of a Straight Line is given by:-

`color(green)((y - y_1) = m(x-x_1))` Formula.1

We can substitute the value of `Slope(m) = 9/7` in the equation above.

We also need a Point.

We will choose one the points given to us: `(6, 11)`

This point `(6, 11)` is our `(x_1, y_1)`.

We are ready to use the Point-Slope Equation of a Straight Line using Formula.1

Substitute the values of `m` and `(x_1, y_1)`.

`y-11 = 9/7(x-6)`

`rArr y - 11 = 9/7x-54/7`

`rArr y = 9/7x + 23/7`

Hence, the Equation of a Straight Line passing through the points `color(red)((6, 11), (-1, 2)` is given by:-

`color(blue)(y = 9/7x + 23/7)`

Graph below has the equation of the straight line we found: