Question

What is the equation of the parabola that has a vertex at `(4, 6)` and passes through point `(-7,-8)`?

Answer 1

`y=(-14/121) x^2+112/121 x+502/121`

`color(green)("Some one may be able to demonstrate a simpler method.")`

Explanation:

Known: The equation standard form is `y=ax^2+bx+c`

Using the two points to give simultaneous equations

`-8=a(-7)^2+b(-7)+c`.................................(1)
`" "6=a(4)^2+b(4)+c`............................................(2)

Known that `x_("vertex")=(-1/2)(b/a)`

`=>4=(-1/2)(b/a)`

So `a(2xx4)=-b`

`=> b=-8a`....................(3)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(brown)("Substitute (3) into (1) and (2)")`

`-8=a(-7)^2+(-8a)(-7)+c`
`" "6=a(4)^2+(-8a)(4)+c`

`-8=49a+56a+c`
`" "6=16a-32a+c`

`-8=" "105a+c" "...................(1_a)`
`" "6=-16a+c" "................(2_a)`

`color(brown)("Subtract "(2_a)" from "(1_a))`

`-14=121a`

`color(blue)(a=-14/121)`
,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)(=> b=-8a -> b= (-8)xx(-14/121) =+112/121)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(brown)("Substitute for "a" in "(2_a))`

`" "6=-16(-14/121)+c`

`color(blue)(c=4 18/121 =502/121)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Answer 2

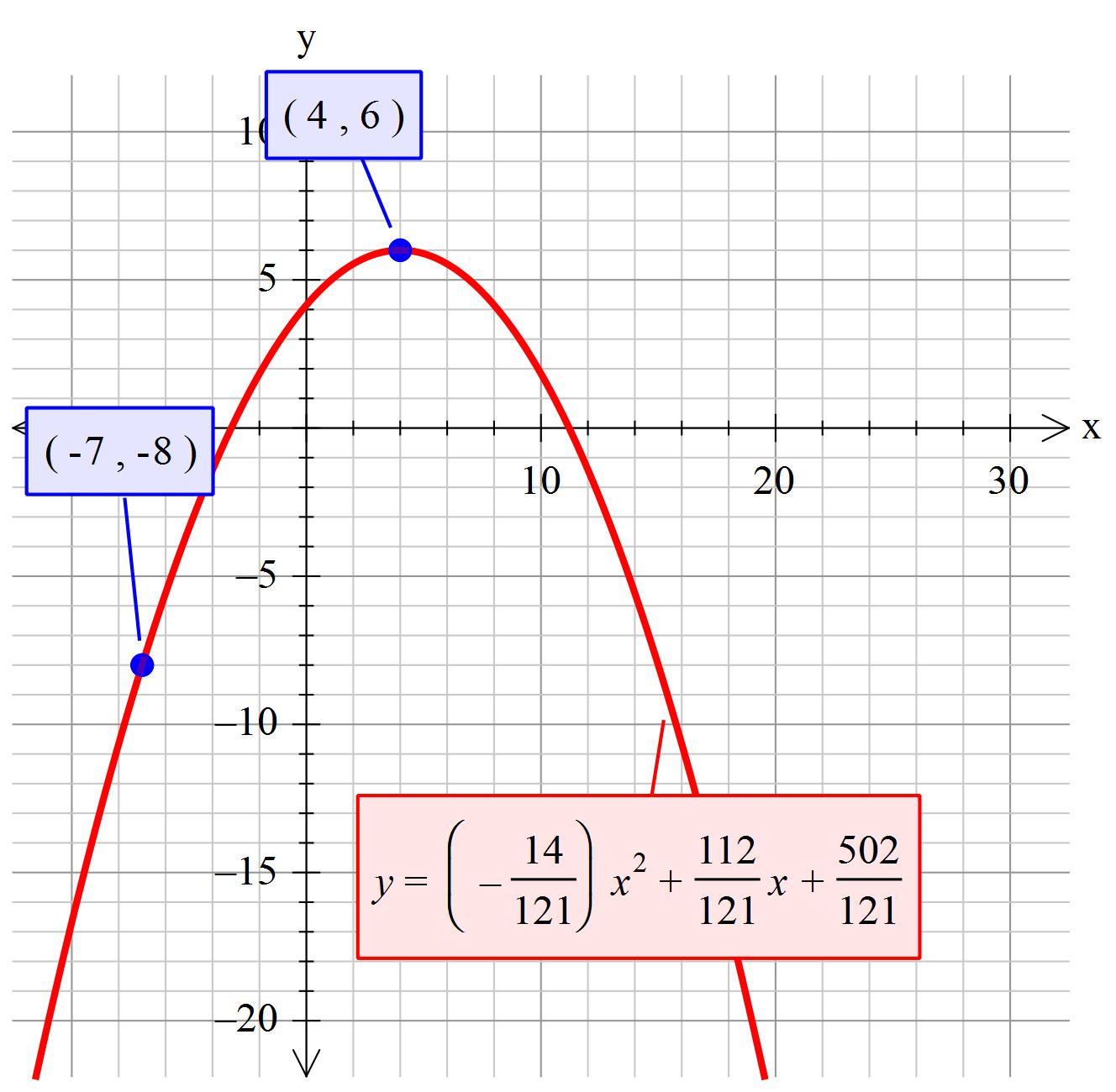
In vertex form:

`y = -14/121 (x-4)^2 + 6`

In standard polynomial form:

`y =-14/121 x^2 + 112/121 x +502/121`

Explanation:

The equation of a parabola with vertical axis can be expressed in vertex form as:

`y = a(x - h)^2 + k`

where `(h, k)` is the vertex and `a` a multiplier.

In our example, the equation of the parabola can be written in the form:

`y = a(x - 4)^2 + 6`

from which we can deduce:

`a = (y-6)/(x-4)^2`

Since we want our parabola to pass through `(-7, -8)` substitute these values of `x` and `y` into this equation to find:

`a = (-8-6)/(-7-4)^2 = -14/121`

So the equation of our parabola may be written:

`y = -14/121 (x-4)^2 + 6`

`=-14/121 x^2 + 112/121 x - 224/121 + 6`

`=-14/121 x^2 + 112/121 x +502/121`

graph{-14/121 x^2 + 112/121 x +502/121 [-20, 20, -10, 10]}