Question

What is the equivalent pressure of 0.743 atm in units of mm Hg?

Answer 1

`"565 mmHg"`

Explanation:

The problem wants you to use a known conversion factor to go from pressure expressed in atmospheres, `"atm"`, to pressure expressed in millimeter of mercury, `"mmHg"`.

Now, you can find the conversion factor that takes you from atmospheres to millimeter of mercury by using the pascals, `"Pa"`, the SI unit of pressure.

In terms of pascals, an atmosphere is defined as a pressure of

`"1 atm " = " 101325 Pa"`

Similarly, a millimeter of mercury, which is simply the pressure exerted by a `"1-mm"` high column of mercury, is defined as a pressure of approximately

`"1 mmHg " ~~ " 133.32239 Pa"`.

Your goal now is to find how many milliliters of mercury are needed to get to the equivalent of one atmosphere. You can say that you have

`overbrace(101325 color(red)(cancel(color(black)("Pa"))))^(color(blue)("= 1 atm")) * "1 mmHg"/(133.32239color(red)(cancel(color(black)("Pa")))) ~~ "760 mmHg"`

This tells you that a column of mercury `"760 mm"` high creates a pressure equal to `"1 atm"`.

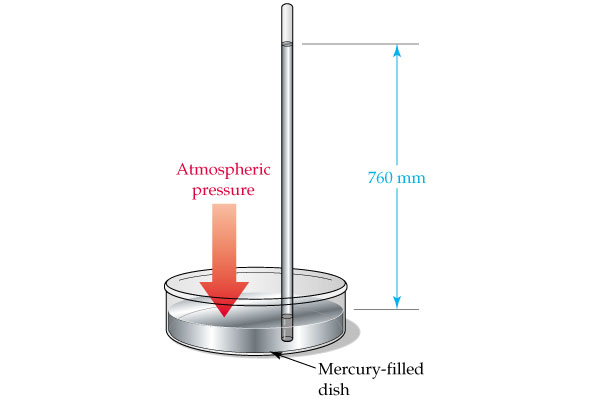
You can thus say that your conversion factor looks like this

`color(purple)(|bar(ul(color(white)(a/a)color(black)("1 atm " = " 760 mmHg")color(white)(a/a)|)))`

Use this conversion factor to find the equivalent pressure of `"0.743 atm"` in units of `"mmHg"`

`0.743 color(red)(cancel(color(black)("atm"))) * "760 mmHg"/(1color(red)(cancel(color(black)("atm")))) = color(green)(|bar(ul(color(white)(a/a)color(black)("565 mmHg")color(white)(a/a)|)))`

The answer is rounded to three sig figs.