What is the equivalent resistance of three resistances of 12 Ω each connected in parallel?
1 Answer
Apr 24, 2015
For the total resistance when the resistors are in parallel to each other, we use:
The situation you describe seems to be this:
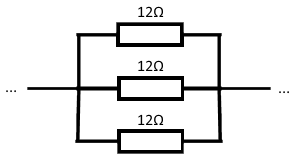
So there are 3 resistors, meaning we will use:
All resistors have a resistance of
Total up the Right Hand Side:
At this point you cross multiply :
Then simply solve it:

