Question

What is the formal definition of a derivative?

Answer 1

The formal definition of derivative of a function `y=f(x)` is:
`y'=lim_(Deltax->0)(f(x+Deltax)-f(x))/(Deltax)`

The meaning of this is best understood observing the following diagram:

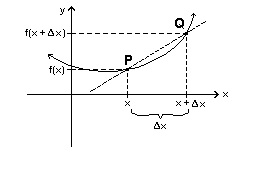
The secant PQ represents the mean rate of change `(Deltay)/(Deltax)` of your function in the interval between `x` and `x+Deltax`.

If you want the rate of change, say, at P you "move" point Q (and the secant with it) to meet point P as in:

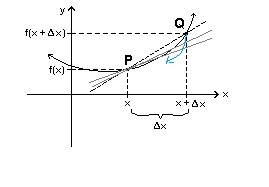
In doing so you must reduce `Deltax`. If `Delta x->0` you'll get the tangent in P whose inclination will give the inclination at P and thus the derivative at P.

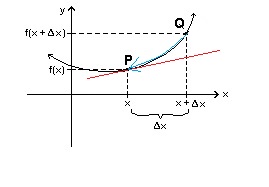
Hope it helps!