The Derivative by Definition
Key Questions
-
First you have to calculate the derivative of the function.
#f(x)=x^3# #f'(x)=3x^2# Then if we want to find the derivative of
#f(x)# when#x=4# then we substitute that value into#f'(x)# .#f'(4)=3(4)^2=3*16=48# -
The formal definition of derivative of a function
#y=f(x)# is:
#y'=lim_(Deltax->0)(f(x+Deltax)-f(x))/(Deltax)# The meaning of this is best understood observing the following diagram:
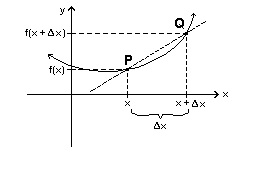
The secant PQ represents the mean rate of change
#(Deltay)/(Deltax)# of your function in the interval between#x# and#x+Deltax# .If you want the rate of change, say, at P you "move" point Q (and the secant with it) to meet point P as in:
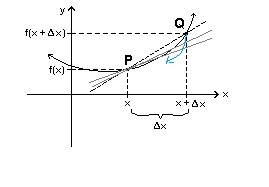
In doing so you must reduce
#Deltax# . If#Delta x->0# you'll get the tangent in P whose inclination will give the inclination at P and thus the derivative at P.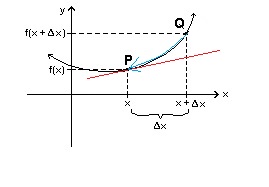
Hope it helps!
-
Answer:
We use quotient rule as described below to differentiate algebraic fractions or any other function written as quotient or fraction of two functions or expressions
Explanation:
When we are given a fraction say
#f(x)=(3-2x-x^2)/(x^2-1)# . This comprises of two fractions - say one#g(x)=3-2x-x^2# in numerator and the other#h(x)=x^2-1# , in the denominator. Here we use quotient rule as described below.Quotient rule states if
#f(x)=(g(x))/(h(x))# then
#(df)/(dx)=((dg)/(dx)xxh(x)-(dh)/(dx)xxg(x))/(h(x))^2# Here
#g(x)=3-2x-x^2# and hence#(dg)/(dx)=-2-2x# and as#h(x)=x^2-1# , we have#(dh)/(dx)=2x# and hence#(df)/(dx)=((-2-2x)xx(x^2-1)-2x xx(3-2x-x^2))/(x^2-1)^2# =
#(-2x^3-2x^2+2x+2-6x+4x^2+2x^3)/(x^2-1)^2# =
#(2x^2-4x+2)/(x^2-1)^2# or
#(2(x-1)^2)/(x^2-1)^2# =
#2/(x+1)^2# Observe that
#(3-2x-x^2)/(x^2-1)=((1-x)(3+x))/((x+1)(x-1))=(-3-x)/(x+1)# and using quotient rule#(df)/(dx)=(-(x+1)-(-3-x))/(x+1)^2=2/(x+1)^2#