The integral of #1/(x^2+a^2)# is given by:
#1/atan^-1(x/a)#
In our case, #a=2# (because #a^2=(2)^2=4#) and #x=x#, of course. Making necessary substitutions into the expression above, we have:
#int 1/(x^2+4)dx=1/2tan^-1(x/2)+C# (never forget the constant #C#)
If you want to see why, I'll describe the process below. I apologize if it gets a bit long, but sometimes calculus can be like that. Feel free to skip over it if it bores you.
First, we note that our denominator, #x^2+a^2#, looks like the Pythagorean theorem: #a^2+b^2=c^2#, the famous equation that describes the relationship between the legs of a right triangle. With that in mind, we can safely assume that #x# and #a# can actually be represented by a right triangle, as shown in the picture below:
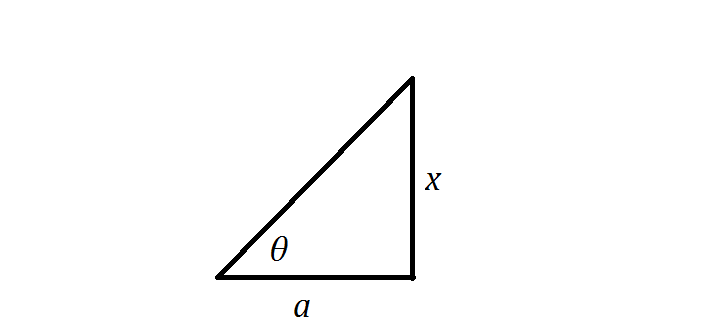
We can see from this picture that the tangent of angle #theta# is equal #x/a#, or #tan(theta)=x/a#. (We use tangent and not sine or cosine because tangent includes both #x# and #a#, and the #x# is in the numerator which makes it look nicer).
If #tan(theta)=x/a#, then by multiplying both sides by #a# we get
#atan(theta)=x#. We can now substitute this expression into the integral to solve it. However, if we replace #x# with #theta#, we must also replace #dx# with #d theta#. We do this by differentiating #atan(theta)=x# with respect to #theta#:
#dx/(d theta)=asec^2(theta)# (because the derivative of #tan(theta)# is #sec^2(theta))#
#dx=asec^2(theta)d theta#
We are now ready to make all substitutions:
#int 1/(x^2+a^2)dx=int 1/(((atan(theta))^2+a^2))*asec^2(theta)d theta#
Now with some simplifying:
#int 1/(x^2+a^2)dx=int (asec^2(theta))/(a^2tan^2(theta)+a^2)d theta#
#int 1/(x^2+a^2)dx=int (asec^2(theta))/(a^2(tan^2(theta)+1))d theta#
#int 1/(x^2+a^2)dx=a/a^2int sec^2(theta)/(tan^2(theta)+1)d theta#
#int 1/(x^2+a^2)dx=1/aint sec^2(theta)/(tan^2(theta)+1)d theta#
If we remember our Pythagorean identities, we know that #tan^2(theta)+1=sec^2(theta)#. Because we have #tan^2(theta)+1# (in the denominator), we can replace it with #sec^2(theta)#:
#int 1/(x^2+a^2)dx=1/aint sec^2(theta)/(sec^2(theta))d theta#
#int 1/(x^2+a^2)dx=1/aint 1d theta#
Our result is #1/a*theta#. However, we need to convert this result back to #x#. How? Earlier, we said #atan(theta)=x#. That means #tan(theta)=x/a#, and furthermore, #theta=tan^-1(x/a)#. Plugging this into our result, we have
#int 1/(x^2+a^2)dx=1/atan^-1(x/a)#
And voila, there you have it.