What is the internal angle sum of a hexagon?

Question

1538 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-16T09:47:38

#720^circ#

First, we split the hexagon into 6 equal isoceles triangles, each have the angles (#60,theta,theta#) (#360/6=60#).

#theta=(180-60)/2=120/2=60#

#"Sum of internal angles"=6(120)=720^circ#

Answer 2 · 2018-05-23T20:23:46

#720^0#

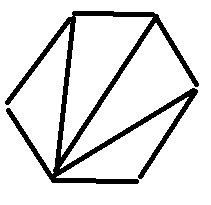
enter image source here

The internal sum of four triangles is #4 times 180^0#

Answer 3 · 2018-06-01T15:17:37

Or, it can be directly calculated using direct formula,

#rarr(n-2)*180^@# where #n# is the number of sides of polygon.

In case of hexagon, #n=6#

So, internal angles sum#=(6-2)*180^@=4*180^@=540^@#