What is the inverse function of #f(x) = cosh(x+a/cosh(x+a/cosh(x+cdots)))# with domain and range?
2 Answers
Explanation:
I confine myself to FCF-naming of the function. For me, the strain is
inevitable.
For this FCF,
The operand is clear in the cosh function, in contrast to either f(x)
or
Inversely,
the inverse of
= the inverse of the equivalent
Now, the inverse is
For a = 1, I use here the inverse for the FCF y = cosh(x+1/y) as
graph that reveals domain and range.
Indeed, x admits negative values.
The graphs for y = f(x) and its inverse
the same.
As any cosh value
The domain/range:
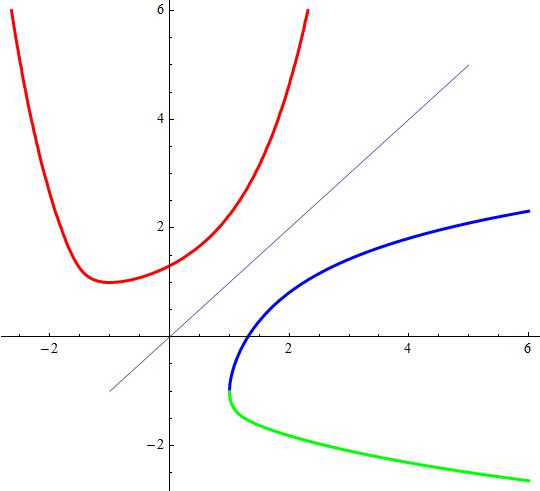
Graph of y = cosh(x + 1/y):
Note that there is no axis of symmetry.
The lowest point (-1, 1) is plotted in the graph.
graph{(x-ln(y+(y^2-1)^0.5)+1/y)(x+ln(y+(y^2-1)^0.5)+1/y)((x+1)^2+(y-1)^2-.004)=0 [-5 5 -1 4]}
Combined graph below, for this and y = cosh x reveals the
patterns.
This graph is my present to those (Caserio, George et al) who had
shown keen interest in FCF.
graph{(x-ln(y+(y^2-1)^0.5)+1/y)(x+ln(y+(y^2-1)^0.5)+1/y)(x-ln(y+(y^2-1)^0.5))(x+ln(y+(y^2-1)^0.5))=0[-5 5 0 10]}
.
Explanation:
From
Finally
then