What is the inverse of #y=3log(5x)-ln(5x^3)#? ?
1 Answer
Jun 22, 2016
Explanation:
Supposing that
For
where
and
Finally
or
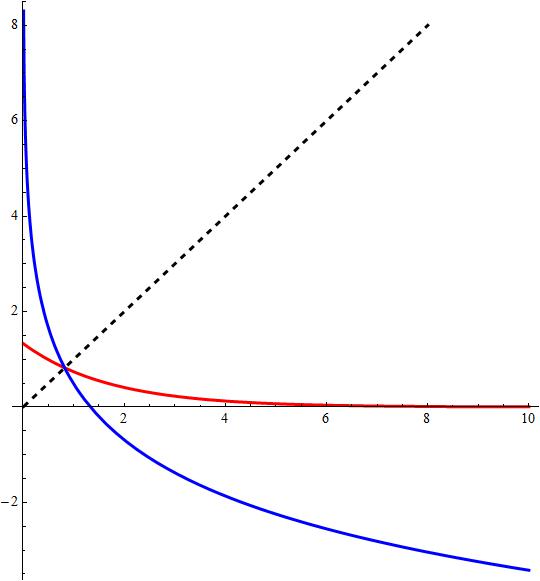
Red
Blue
Supposing that
For
where
and
Finally
or
Red
Blue
