Question

WHat is the largest cylinder of radius, `r` and height `h` that can fit in sphere of radius, `R`?

Answer 1

The maximum volume of the cylinder is found if we choose

`r = sqrt(2/3)R`, and `h = (2R)/sqrt(3)`

This choice leads to a maximum cylinder volume of:

`V=(4pi R^3)/(3sqrt(3))`

Explanation:

``

Imagine a cross section through the centre of the cylinder, and let the cylinder have height `h`, and volume `V`, then we have;

`h` and `r` can be varied and `R` is a constant. The volume of the cylinder is given by the standard formula :

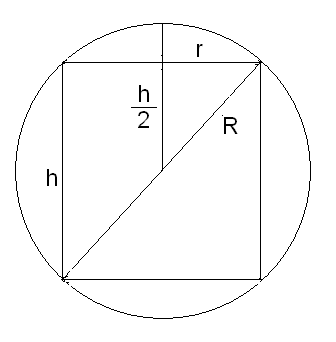
`V=pir^2h`

The radius of the sphere, `R` is the hypotenuse of the triangle with sides `r` and `1/2h`, so using Pythagoras, we have:

`\ \ \ \ \ R^2=r^2+(1/2h)^2`
`:. R^2=r^2+1/4h^2`
`:. \ r^2=R^2-1/4h^2`

We can substitute this into our volume equation to get:

`\ \ \ \ \ V=pir^2h`
`:. V=pi( R^2-1/4h^2 )h`
`:. V=pi R^2h-1/4pih^3`

We now have the volume, `V` as a function of a single variable `h`, which we seek to maximise wrt `h` so differentiating wrt `h` gives:

`(dV)/(dh)=pi R^2-3/4pih^2`

At a minimum or maximum, `(dV)/(dh)=0` so:

`pi R^2-3/4pih^2 = 0`
`:. \ \ \ \ \ \ \ \ \3/4h^2 = R^2`
`:. \ \ \ \ \ \ \ \ \ \ \ \h^2 = 4/3 R^2`
`:. \ \ \ \ \ \ \ \ \ \ \ \ \ \h = sqrt(4/3 R^2) " "` (obviously we want te +ve root)
`:. \ \ \ \ \ \ \ \ \ \ \ \ \ \h = (2R)/sqrt(3)`

With this value of `h` we get:

`\ \ \ \ \ \ r^2 = R^2-1/4 4/3 R^2`
`:. \ r^2 = R^2-1//3 R^2`
`:. \ r^2 = 2/3R^2`
`:. \ \ r = sqrt(2/3)R`

We should check that this value leads to a maximum (rather than a maximum) volume, We do this by looking at the second derivative:

`(dV)/(dh)=pi R^2-3/4pih^2`
`:. (d^2V)/(dh^2) = -6/4pih`

And as `h>0` we conclude that `(d^2V)/(dh^2) < 0` and that the critical point identified leads to a maximum as sought.

Hence, the maximum volume of the cylinder is found if we choose

`r = sqrt(2/3)R`, and `h = (2R)/sqrt(3)`

With this choice we get the maximum volume as;

`V=pi R^2((2R)/sqrt(3) ) -1/4pi((2R)/sqrt(3))^3`
`:. V=(2pi R^3)/sqrt(3) - 1/4pi((8R^3)/(3sqrt(3)))`
`:. V=(2pi R^3)/sqrt(3) - (2piR^3)/(3sqrt(3))`
`:. V=(4pi R^3)/(3sqrt(3))`

And obviously the volume of the Sphere is given by:

`V_s = 4/3piR^3`

This is a very famous problem, that was studied by Greek mathematicians way before Calculus was discovered. An interesting property is the ratio of the volume of the cylinder to the volume of the sphere:

`V/V_s = ((4pi R^3)/(3sqrt(3))) / (4/3piR^3) = 1/sqrt(3)`

In other words the ratio of the volumes is completely independent of `R`, `r` or `h` which is quite an astounding result!