What is the length of the side of a square whose diagonal is 10?
1 Answer
Apr 12, 2016
Draw a diagram to represent your situation.
Explanation:
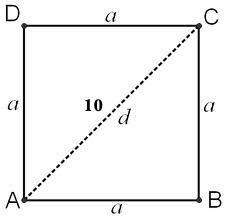
Since we're dealing with a square, all side lengths measure the same thing. Furthermore, the angle B and D are right, therefore allowing us to use pythagorean theorem to find the value of a.
#color(blue)(a^2 + b^2 = c^2#
Where
Since
The diagonal is the Hypotenuse
So, the side lengths measure
Hopefully this helps!


