Question

What is the maximum area of a rectangle that can be circumscribed about a given rectangle with length L and width W?

Answer 1

`1/2(L+W)^2`

Explanation:

Let us set up a concrete scenario...

Start with a rectangle with vertices:

`(L/2, W/2)`

`(-L/2, W/2)`

`(-L/2, -W/2)`

`(L/2, -W/2)`

Rotate it anticlockwise about the origin by `theta` to give a rectangle with vertices:

`(L/2 cos theta - W/2 sin theta, W/2 cos theta + L/2 sin theta)`

`(-L/2 cos theta - W/2 sin theta, W/2 cos theta - L/2 sin theta)`

`(-L/2 cos theta + W/2 sin theta, -W/2 cos theta - L/2 sin theta)`

`(L/2 cos theta + W/2 sin theta, -W/2 cos theta + L/2 sin theta)`

(For simplicity, just consider `0 <= theta <= pi/2` so we don't have to be concerned about a variety of cases, etc.)

Then the circumscribing rectangle with sides parallel to the `x` and `y` axes has area:

`(L cos theta + W sin theta)(W cos theta + L sin theta) = (L^2+W^2)cos theta sin theta+WL`

`color(white)((L cos theta + W sin theta)(W cos theta + L sin theta)) = 1/2(L^2+W^2)sin 2theta+WL`

This takes its maximum value when `sin 2theta = 1`, e.g. when `theta = pi/4`

So the maximum area is:

`WL+1/2(L^2+W^2) = 1/2(L+W)^2`

Unsurprisingly, this is when the circumscribing rectangle is a square.

Answer 2

`1/2(L+ W)^2`

Explanation:

Now using the Lagrange Multipliers technique.

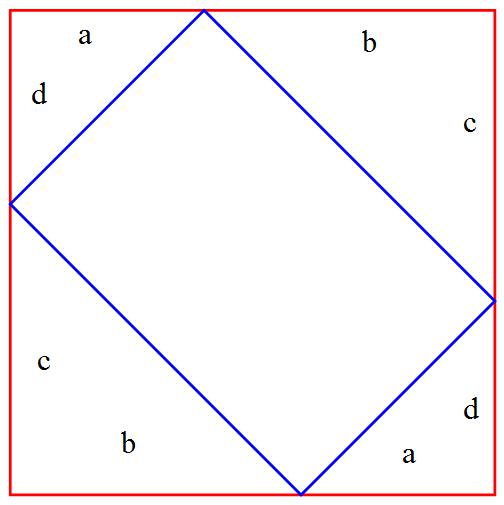
The circumscribed rectangle has the side dimensions

`(a+b)` and `(c+d)` so the sough area is `(a+b)(c+d)`

The restrictions are

`a^2+b^2=L^2` and
`c^2+d^2=W^2`

The lagrangian is

`Phi(a,b,c,d,lambda_1,lambda_2)=(a+b)(c+d)+lambda_1(a^2+b^2-L^2)+lambda_2(c^2+d^2-W^2)`

The stationary points are the solutions of

`grad Phi=(Phi_a,Phi_b,Phi_c,Phi_d,Phi_(lambda_1),Phi_(lambda_2))=0`

or

`{(c + d + 2 a lambda_1=0),(c + d + 2 blambda_2=0),(a + b + 2 c lambda_2=0),(a + b + 2 d lambda_1=0),(a^2 + d^2 - L^2=0),(b^2 + c^2 - W^2=0):}`

Solving for `a,b,c,d,lambda_1,lambda_2` we get at

`((a=L/sqrt[2]),(b=W/sqrt[2]),(c=W/sqrt[2]),(d=L/sqrt[2]),(lambda_1=-(L +W)/(2 L)),(lambda_1=-(L +W)/(2 W)))`

and the maximum area is

`(a+b)(c+d)=1/2(L+ W)^2`

Of course the minimum area circumscribing rectangle has the area `L cdot W`

Answer 3

`1/2(L+W)^2`

Explanation:

And now with rotations.

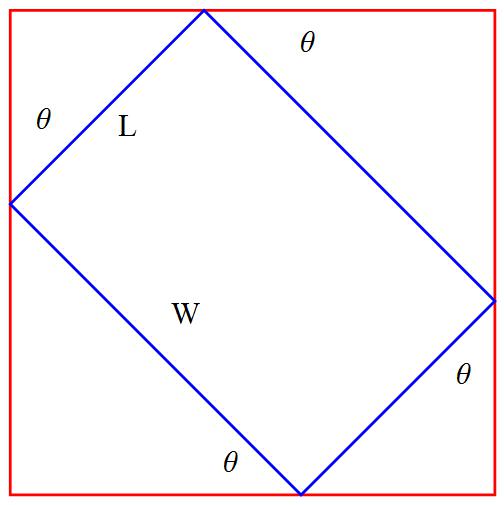
The circumscribed quadrilateral area is given by

`A(theta)=2(1/2(Wsintheta)(Wcostheta)+1/2(Lsintheta)(Lcostheta))+LW`

so

`A(theta)=(W^2+L^2)sintheta costheta+LW`

Now the maximum is at the solution of

`(dA)/(d theta) = (W^2+L^2)(1-2sin^2theta)=0`

giving `theta={-3pi/4,-pi/4,pi/4,3pi/4}`. Between those solutions we will choose the maximum. The local maxima are located at points in which `(d^2A)/(d theta^2) < 0`

so the solution is for `theta=pi/4` or `theta=-3pi/4`

`A(pi/4)=(W^2+L^2)(1/sqrt(2))^2+LW=1/2(L+W)^2`

because at this point

`(d^2A)/(d theta^2)=-4(W^2+L^2)costheta sintheta=-2(W^2+L^2)<0`