What is the meaning of the limit of a function?
1 Answer
The statement
Explanation:
The precise definition is:
For any real number
Consider the function
If we plot the graph, it looks like this:
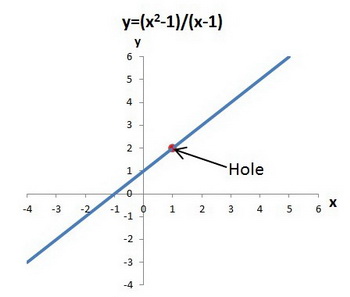
We can't say what the value is at
Let's try to show that
The question is, how do we get from
We must start with some value of
Let's start with
The other condition is
The definition fits exactly if
We have just shown that for any
So we have shown that

