Concepts and Informal Definition of a Limit

Key Questions

  • How do I find a limit by looking at the graph?

    Answer:

    I am not sure if it is helpful but I use this from my old maths book:

    Explanation:

    Have a look:
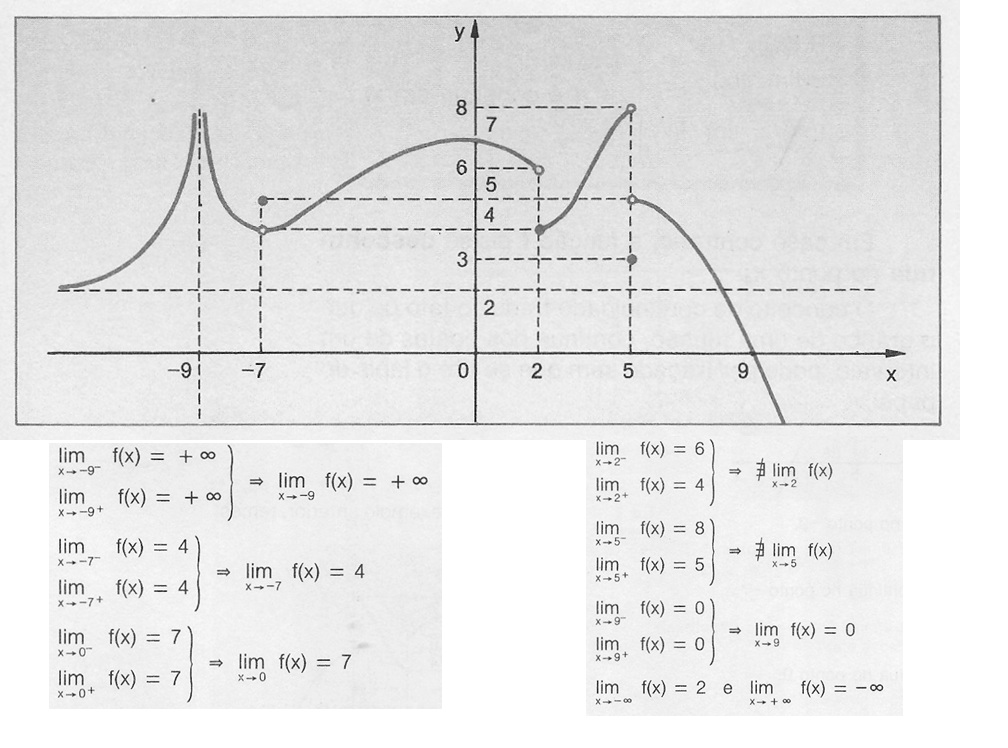
    enter image source here

    Gió · 1 · Sep 26 2015
  • How do I find a limit algebraically?

    Answer:

    A few thoughts...

    Explanation:

    This is not always feasible, but there are some cases that work.

    If #f(x)# is a polynomial function, then we can find limits for finite values by substitution:

    #lim_(x->a) f(x) = f(a)#

    For example:

    #lim_(x->2) (x^5+4x+2) = (color(blue)(2))^5+4(color(blue)(2))+2 = 32+8+2 = 42#

    Sometimes it helps to use some kind of radical conjugate. For example:

    #lim_(x->oo) x(sqrt(x^2+1) - sqrt(x^2-1))#

    #= lim_(x->oo) (x(sqrt(x^2+1) - sqrt(x^2-1))(sqrt(x^2+1) + sqrt(x^2-1)))/(sqrt(x^2+1)+sqrt(x^2-1))#

    #= lim_(x->oo) (x((color(red)(cancel(color(black)(x^2)))+1) - (color(red)(cancel(color(black)(x^2)))-1)))/(sqrt(x^2+1)+sqrt(x^2-1))#

    #= lim_(x->oo) 2/(sqrt(1+1/x^2)+sqrt(1-1/x^2))#

    #= 2/(1+1)#

    #= 1#

    However, note that functions are not necessarily defined as #f(x) = ...# or #y = ...#. For example, consider the equation:

    #y^5+4y+2 = x#

    This defines #y# as a function - let's call it #g(x)# - of #x#, since #x^5+4x+2# is continuous and strictly monotonically increasing, so has a continuous monotonic inverse.

    Then we find that:

    #lim_(x->0) g(x)#

    is the root of #x^5+4x+2 = 0#, which is not expressible in terms of elementary functions. It is only really practical to evaluate approximations to it using numerical methods.

    So there really is no general method that will work in all cases.

    George C. · 1 · Jul 31 2018

Questions

Limits